How To Find Angles Of Congruent Triangles

To summarize congruent figures are identical in size and shape. They can be rotated reflected or translated and still be congruent.

Puzzle Sheet Geometry Worksheets Congruent Triangles Worksheet Math Geometry

The side lengths and angles are the same.

How to find angles of congruent triangles. The Three Angles Add to 180 Exterior Angle Theorem. The Law of Cosines. Since two congruent triangles will combine to form a square or other quadrilateral the sum of the angles in one of the triangles is half of 360 or 180.

Theorems about Similar Triangles. This describes the algorithm behind the angle-finder calculator above. The Shapes and Sizes of Pythagorean Triangles P Shiu Mathematical Gazette vol.

The sum of the angles in a triangle is 180. To find a Pythagorean triangle with angles close to θ let u tanθ secθ and find its continued fraction. How to Find if Triangles are Similar.

The Law of Sines. The sum of the angles in a square or other quadrilateral is 360. Here the same two figures are congruent with one translated up and away from the other.

And here are the same two congruent figures with one of them reflected flipped. 67 1983 pages 33-38.

Read more »

What Is A Congruence Statement For The Following Congruent Triangles

A B A ABC AEDF A ABC ADEF Ο ΔΑΒC 2 ΔΕPD A ABC AFED None Of These Is A Correct Congruence Statement. The ASA Postulate was contributed by Thales of Miletus Greek.

Triangle Congruence 4 Mazes Sss Sas Asa Aas Hl Geometry Lessons Teaching Geometry Geometry Worksheets

We use the symbol to show congruence.

What is a congruence statement for the following congruent triangles. Angle C Angle F Of course Angle A is short for angle BAC etc Very Important Remark about Notation ORDER IS CRITICAL. Name the two congruent triangle and name the congruent corresponding arts. Is it SSS SAS ASA or AAS.

J M K N L O. P 23 We M 23 N. Under this criterion if the two angles and the side included between them of one triangle are equal to the two corresponding angles and the side included between them of another triangle the two triangles are congruent.

This means that congruent triangles are exact copies of each other and when fitted together the sides and angles which coincide called corresponding sides and angles are equal. This means that the corresponding sides are equal and the corresponding angles are equal. Congruent Triangles do not have to be in the same orientation or position.

Angle m is congruent to angle H. We say that triangle ABC is congruent to triangle DEF if. Write a congruence statement for angle m.

Complete the congruence statement. In a squared sheet draw two triangles of equal areas such that i the triangles are congruent. Angle A Angle D.

What can you say about their perimeters. Definition of Triangle Congruence. Which Of The Below Statements Is A Correct Congruence Statement.

This concept teaches students how to write congruence statements and use congruence statements to determine the corresponding parts of triangles. Given the following statement which angle is congruent to angle W Given the following statement which side is congruent to VU Given the following statement which side is congruent to IG Use the diagram to identify which side is congruent to CB. Ii the triangles are not congruent.

Question 2 5 Points Listen Consider Two Congruent Triangles Such That ABC - AXyz And The Following. They only have to be identical in size and shape. Angle B Angle E.

Isosceles and Equilateral Triangles. Andre drew four congruent triangles with legs a and b units long and hypotenuse c. If repositioned they coincide with each other.

Draw the two congruent triangles using only the 3 pairs of congruent corresponding angle. 1 A B C is congruent to D E F. What are the 7 classifications of triangles SAS SSSetc and 5 triangle congruence postulates.

Write a congruence statement for the two triangles. The symbol of congruence is. Which triangle congruence theorem explains why all triangles are rigid.

Corresponding sides and angles mean that the side on one triangle and. If two pairs of angles of two triangles are equal in measurement and the included sides are equal in length then the triangles are congruent. Congruent triangles are triangles that have the same size and shape.

How many pairs of corresponding parts are congruent if two triangles are congruent. These triangles can be slides rotated flipped and turned to be looked identical. If three pairs of sides of two triangles are equal in length then the triangles are congruent.

ASA Criterion for Congruence ASA Criterion stands for Angle-Side-Angle Criterion. A Summary of Triangle Congruence. Write the congruence statement for each pair of congruent triangles.

If 7x21 then x. Two triangles are said to be congruent if one can be placed over the other so that they coincide fit together. Two triangles are congruent if their corresponding sides are equal in length and their corresponding interior angles are equal in measure.

Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure.

Read more »

Which Statements Are Properties Of Right Triangles

Thus these are properties that are unique to. An inverse power of three multiple of the original length.

Stay In Shape Activity Teachengineering

Types and Properties Properties of Shapes.

Which statements are properties of right triangles. Each indicates a justification of a construction or conclusion in a sentence to its left. Grade 6 Geometry Solve real-world and mathematical problems involving area surface area and volume. 1 Print this page.

Rectangles Squares and Rhombuses Diagonals of Quadrilaterals. AAA works fine to show that triangles are the same SHAPE similar but does NOT work to show congruence. Properties Perimeter of the Koch snowflake.

CCSSMathContent8GA5 Use informal arguments to establish facts about the angle sum and exterior angle of triangles about the angles created when parallel lines are cut by a transversal and the angle-angle criterion for similarity of triangles. If the original equilateral triangle has sides of length s the length of each side of the snowflake after n iterations is. For example arrange three copies of the same triangle so that the sum of the three angles appears to form a line and give an argument in terms.

You can draw 2 equilateral triangles that. They are not part of Euclids Elements but it is a tradition to include them as a guide to the reader. The abbreviations in the right column refer to postulates definitions common notions and previously proved propositions.

Remember that if we know two sides of a right triangle we know the third side anyway so this is really just SSS. A triangle ABC that has the sides a b c semiperimeter s area T exradii r a r b r c tangent to a b c respectively and where R and r are the radii of the circumcircle and incircle respectively is equilateral if and only if any one of the statements in the following nine categories is true. Each iteration multiplies the number of sides in the Koch snowflake by four so the number of sides after n iterations is given by.

Find the area of right triangles other triangles special quadrilaterals and polygons by composing into rectangles or decomposing into triangles and other shapes. Apply these techniques in the context of solving real-world and mathematical problems. Lesson for Kids.

Read more »

How To Determine Congruent Triangles

The two sides of the triangles are equal. Side Angle Side SAS is a rule used to prove whether a given set of triangles are congruent.

Proving Triangles Congruent With Congruence Shortcuts Proving Triangles Congruent Geometry Lessons Teaching Geometry

Complete the explanation of your reasoning.

How to determine congruent triangles. Two or more triangles are said to be congruent if they have the same shape and size. Triangles are congruent when all corresponding sides interior angles are congruent. Solution for Determine whether the triangles are congruent.

2 triangles are congruent if they have. Given two triangles determine whether they are congruent and use that to find missing angle measures. Exactly the same three sides and.

The triangles will have the same size shape but 1 may be a mirror image of the other. Also it is clear that the two vertically opposite angles are equal. Learn how to solve for unknown variables in congruent triangles.

Learn how to solve for unknown variables in congruent triangles. Two or more triangles are said to be congruent if they have the same shape and size. Learn how to solve for unknown variables in congruent triangles.

Illustration of SAS rule. So it doesnt follow SAS congruence criteria. Remember that the included angle must be formed by the two sides for the triangles to be congruent.

In this case two triangles are congruent if two sides and one included angle in a given triangle are equal to the corresponding two sides and one included angle in another triangle. Given two triangles determine whether they are congruent and use that to find missing angle measures. If youre seeing this message it means were having trouble loading external resources on our website.

Two or more triangles are said to be congruent if they have the same shape and size. Use the triangle congruence criteria SSS SAS ASA and AAS to determine that two triangles are congruent. B Mark the congruent sides in the quadrilateral.

If they are congruent give the justification and give the triangle congruence statement. Use the triangle congruence criteria SSS SAS ASA and AAS to determine that two triangles are congruent. Determine if the triangles are congruent.

If youre seeing this message it means. Step 2 Therefore two sides and one angle of the triangles are equal. If the three sides of one triangle are congruent to the three sides of another triangle then the triangles are congruent Side-Side-Side or SSS.

For 4 and 5 mark the sides andor angles that you know are congruent from the given information. What else should you know is true without being told. To PR by the v to QR because PS.

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle then the triangles are congruent Side-Angle-Side or SAS. Determine congruent triangles practice Khan Academy. But the triangles are not congruent because the angle isnt between the two equal sides as per SAS congruence criteria.

Frac msquare msquare x2.

Read more »

Can You Use Aas To Prove Triangles Congruent

The triangles are congruent by the AAS Congruence Theorem. The vertical angles are congruent so two pairs of angles and a pair of non-included sides are congruent.

Proving Triangles Congruent With Congruence Shortcuts Proving Triangles Congruent Geometry Lessons Teaching Geometry

Two pairs of corresponding sides are congruent.

Can you use aas to prove triangles congruent. HL right A only The hypotenuse and one of the legs are congruent. A Name four pairs of vertical angles. AAS Angle-Angle-Side If two angles and a non-included side in one triangle are congruent to two angles and the corresponding non-included side in another triangle then the triangles are congruent.

SSS SAS ASA AAS and HL. 8 7 6 5 4 3 2 1 Name. AAS Two angles and a non- included side are congruent.

By the reflexive property of congruence SQ SQ. B A Y X. SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal.

You can now conclude that nPSQ nRQS by the SAS Congruence Postulate. In the figure above the two triangles above are initially congruent. SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal.

Geometry Notes G6 ASA AAS Use Congruent Triangles Mrs. Angle Side Angle Triangle The term angle-side-angle triangle refers to a triangle with known measures of two angles and the length of the side between them. A Explain how you would use the given information and congruent triangles to prove the statement.

Whereas the Angle-Angle-Side Postulate AAS tells us that if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle then the two triangles are congruent. Can you use the SAS Postulate the AAS Theorem or both to prove the triangles congruent. There are five ways to find if two triangles are congruent.

Can you use the ASA Postulate or the AAS Theorem to prove the triangles congruent. Either SAS or AAS B. SAS side angle side.

But if you click on Show other triangle you will see that there is another triangle that is not congruent but that still satisfies the SSA condition. In the diagram you can see that STV and QUV are right angles. Sometimes when you are trying to decide if triangles are congruent you need to identify other sides or angles that are congruent.

Triangle Congruence Postulates and Theorems You have learned five methods for proving that triangles are congruent. ASA angle side angle. You can use the AAS Congruence Theorem to prove that EFG JHG.

I can prove triangles congruent using AAS. ZV ZY WZ is the perpendicular bisector of vy. SSS SAS ASA AAS and HL.

There are five ways to find if two triangles are congruent. Pair of corresponding sides are congruent. If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non included side of a second triangle then the triangles are congruent.

This is not enough information to. Sss All three sides are congruent. Favorite Answer You can prove it using ASA as well but it isnt as obvious as AAS.

B Name four pairs of corresponding angles. Grieser Page 2 Use Congruent Triangles to Prove Corresponding Parts Congruent CPCTC can be used to show corresponding parts of congruent triangles congruent Examples. Angle-Angle Side Congruence Theorem.

Alternate Interior Angles Theorem you can conclude that RQS PSQ. Yes we can use both ASA Postulate or the AAS Theorem to prove the triangles congruent. SAS side angle side ASA angle side angle.

By the definition of a right triangle you can conclude that nSTV and. SAS Two sides and the included angle are congruent. BIn addition to the congruent segments that are marked NP Æ NPÆ.

AB is the same. Since vertical angles are congruent we see that the middle. But there are two triangles possible that have the same values so SSA is not sufficient to prove congruence.

_____ Unit 8 Day 3 - Proving Triangles Congruent Classwork 1. ASA postulate says that if two angles and the included side of a triangle are congruent to the corresponding parts of another triangle then the triangles are congruent.

Read more »

How To Prove Similar Triangles In A Circle

Since these angles are congruent the triangles are similar by the AA shortcut. Create your free account Teacher Student.

Circle Theorems Geometry Circle Theorems Theorems Teaching Geometry

The length of the remaining side follows via the Pythagorean Theorem.

How to prove similar triangles in a circle. KM x LB LM x KD. And I take the triangle COY with angles 30-60-90. If also their corresponding sides are parallel they are said to be similarly situated or homothetic Theorem 1 The ratio of the areas of similar triangles or polygons is equal to the ratio of the squares on corresponding sides.

All radii are the same in a particular circle. Two triangles in a circle are similar if two pairs of angles have the same intercepted arc. Designate the legs of length a and b and hypotenuse of length c.

Sharing an intercepted arc means the inscribed angles are congruent. A a b b Step 4. Inscribed in a semi right 23.

Recognise that each small triangle has two sides that are radii. Lets say we have a circle and then we have a diameter of this circle let me drew my best draw my best diameter thats pretty good this right here is the diameter of the circle er its a diameter of the circle thats the diameter and lets say I have a triangle where the diameter is one side of the triangle and the angle opposite that side its vertex sits someplace on the circumference so lets say the angle or the angle opposite of this diameter sits on that circumference so the triangle. Angles in isosceles triangles Because each small triangle is an isosceles triangle they.

Sharing an intercepted arc means the inscribed angles are congruent. How to Prove that Triangles are Similar 1. Show your work for all calculations.

Since these angles are congruent the triangles are similar by the AA shortcut. Show that all circles are similar using similar triangles From LearnZillion Created by Leah Weimerskirch Standards. Tangent Radius or Diameter at point of contact 1 Methods of Proving Triangles Similar.

To develop a plan reason backwards from the prove by answering three questions 1. If a pair of triangles have three proportional corresponding sides then we can prove that the triangles are similar. Since these angles are congruent the triangles are similar by the AA shortcut.

Two triangles in a circle are similar if two pairs of angles have the same intercepted arc. If there are corresponding angles between parallel lines they are congruent. The two students have different methods.

Similar Circles Journal Geometry Points Possible. In this lesson you will learn to show that all circles are similar by using similar triangles. Create a new teacher account for LearnZillion.

Sharing an intercepted arc means the inscribed angles are congruent. Two triangles in a circle are similar if two pairs of angles have the same intercepted arc. This means that each small triangle has two sides the same length.

ABCD is a parallelogram Prove. If there are vertical angles they are congruent. Prove That All Circles Are Similar Instructions View the video found on page 1 of this Journal activity.

Congruent triangles are ones that have three identical sides. Using the information provided in the video answer the questions below. The side opposite the 30 angle is half of a side of the equilateral triangle and hence half of the hypotenuse of the 30-60-90 triangle.

If there are congruent triangles all their angles are congruent. ABC and PQR are similar triangles and AD and PS are their heights. The Pythagorean Theorem states that the sum of squares of the two legs of a right triangle is equal to the square of the hypotenuse so we need to prove a2 b2 c2.

Since OC 1 then OY. Products involving Line Segments. Students will be able to prove.

The reason is because if the corresponding side lengths are all proportional then that will force corresponding interior angle measures to be congruent which means the triangles will be similar. Proportions involving Line Segments. Methods of Proving Triangles Similar Day 2.

They must therefore both be isosceles triangles.

Read more »

What Is Angle Bisector Theorem In Triangles

What is the Triangle Angle Bisector Theorem. This is the currently selected item.

Pin On Geometry Technology Based Lessons Activities Ideas For Teachers

As per the Angle Bisector theorem the angle bisector of a triangle bisects the opposite side in such a way that the ratio of the two line-segments is proportional to the ratio of the other two sides.

What is angle bisector theorem in triangles. The 45-45-90 triangle has three unique properties that make it very special and unlike all the other triangles. Here AD is the bisector of A A. Triangle angle bisector theorem states that In a triangle the angle bisector of any angle will divide the opposite side in the ratio of the sides containing the angle.

It equates their relative lengths to the relative lengths of the other two sides of the triangle. As you can see in the picture below the angle bisector theorem states that the angle bisector like segment AD in the picture below divides the sides of the a triangle proportionally. So we get angle ABF angle BFC alternate interior angles are equal.

According to the angle bisector theorem BD DC AB AC B D D C A B A C. Consider the figure below. Proof of Triangle Angle Bisector.

Triangle Angle Bisector Theorem States that an angle bisector of a triangle divides the interior angles opposite side into two segments that are proportional to the other two sides of the triangle. Using the angle bisector theorem. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.

As the sum of all interior angles of a triangle is 180 degrees then the sum of two interior angles cannot be equal to 360 in measure and therefore the angle bisectors cannot be parallel. What is the Angle Bisector theorem. Draw B E A D.

Triangle Angle Bisector Theorem. The Angle-Bisector theorem involves a proportion like with similar triangles. If a ray bisects an angle of a triangle then it divides the opposite side of the triangle into segments that are proportional to the other two sides.

The following figure gives an example of the Angle Bisector Theorem. Triangle Angle Bisector Theorem file name. Solving problems with similar congruent triangles.

45-45-90 triangles are special right triangles with one 90 degree angle and two 45 degree angles. Then BDDC ABAC. Thus the relative lengths of the opposite side divided by angle bisector are equated to the lengths of the other two sides of the triangle.

An angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle. Now CF is parallel to AB and the transversal is BF. This is called the Angle Bisector Theorem.

Using the angle bisector theorem. By the Angle Bisector Theorem B D D C A B A C. We know that BD is the angle bisector of angle ABC which means angle ABD angle CBD.

In ΔABC If AD bisects BAC. The picture below shows the proportion in action. All 45-45-90 triangles are considered special isosceles triangles.

If ratios are perfectly equal to each other the line segment is the angle bisector. An angle bisector cuts an angle exactly in half. The angle bisector theorem is concerned with the relative lengths of the two segments that a triangles side is divided into by a line that bisects the opposite angle.

Extend C A to meet B E at point E. Same as angle ABF. The Angle-Bisector theorem states that if a ray bisects an angle of a triangle then it divides the opposite side into segments that are proportional to the other two sides.

By the Side-Splitter Theorem. One important property of angle bisectors is that if a point is on the bisector of an angle then the point is equidistant from the sides of the angle. The theorem was proposed by Robert Simson and he proved the theorem in a perfect defined way.

Intro to angle bisector theorem. The following figure illustrates this. But we already know angle ABD ie.

Read more »

Proving Triangles Congruent Asa Aas And Hl

In another lesson we will consider a proof used for right triangles called the Hypotenuse Leg rule. SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal.

Congruent Triangles Methods Of Proving Triangles Congruent Proof Practice Teaching Geometry Proving Triangles Congruent Geometry Worksheets

In this lesson we will consider the four rules to prove triangle congruence.

Proving triangles congruent asa aas and hl. AAS Two angles and the non-included side of one triangle are congruent to two angles and the non-included side of another triangle. If the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of another right triangle then the triangles are congruent Hypotenuse-Leg or HL. As long as one of the rules is true it is sufficient to prove that the two triangles are congruent.

Improve your math knowledge with free questions in Proving triangles congruent by SSS SAS ASA and AAS and thousands of other math skills. Choose 5 key terms from this unit that you. There are five ways to find if two triangles are congruent.

When proving two triangles are congruent you use information and postulates you already know to create a logical trail from what you know to what you want to show. What about the others like SSA or ASS. The ASA criterion for triangle congruence states that if two triangles have two pairs of congruent angles and the common side of the angles in one triangle is congruent to the corresponding side in the other triangle then the triangles are congruent.

SSS SAS ASA AAS and HL. If three sides of one triangle are equal to three sides of another triangle the triangles are congruent. How do we prove triangles congruent.

State what additional information is required in order to know that the triangles are congruent for the reason given. There are five ways to find if two triangles are congruent. If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of another triangle then the triangles are congruent Angle-Angle-Side or AAS.

When proving two triangles are congruent you use information and postulates you already know to create a logical trail from what you know to what you want to show. The SAS Postulate tells us If two sides and the included angle of a triangle are congruent to two sides and the included angle of another triangle then the two triangles are congruent. HUG and LAB each have one angle measuring exactly 63.

Start studying Proving Triangles Congruent by SSS SAS ASA AAS or HL. SSS SAS ASA AAS and HL. Learn vocabulary terms and more with flashcards games and other study tools.

HL Hypotenuse leg The hypotenuse and leg of one right triangle is congruent. Geometry A Unit 6 Congruent Triangles I. We continue our lessons on proving triangles are congruent using ASA AAS HL.

SAS side angle side ASA angle side angle. Angle Angle Side AAS Hypotenuse Leg HL CPCTC. These theorems do not prove congruence to learn more click on the links.

Corresponding Sides and Angles. Solution for Triangle Congruence ASA AAS HL 2 of 3 Use deductive reasoning to show that the two triangles are congruent Given that ZFAB LGED and C is the. For each pair to triangles state the postulate or theorem that can be used to conclude that the triangles are congruent.

Exactly the same three sides and. They are called the SSS rule SAS rule ASA rule and AAS rule. For each set of triangles above complete the triangle congruence statement.

Sides h and l. This tutorial shows an example of using a congruence postulate to show two triangles are congruent. ASA SAS SSS Hypotenuse Leg Preparing for Proof.

Proving Triangles Congruent by ASA AAS and HL How Do You Use a Congruence Postulate to Prove Triangles are Congruent. ASA works because there is one and only one triangle that can be drawn with specific angle side angle information. SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal.

Either side that is not between the two angles being used is can be a non-included side. Identify congruent figures and corresponding parts of congruent figures Prove that two triangles are congruent using various methods such as SSS SAS ASA AAS and HL Prove that parts of two triangles are congruent Identify and use properties of isosceles and equilateral triangles II. 11 ASA E C D Q 12 ASA K L M U S T 13 ASA R T S E C 14 ASA U W V M K 15 AAS E D C T 16 AAS Y X Z L M N 17 ASA G I V H 18 AAS J K L F-2-.

Sss sas asa aas and hl. The side between the two angles being used is the included side. Worksheets on Triangle Congruence.

Corresponding sides g and b are congruent. Popular Tutorials in Proving Triangles Congruent by ASA AAS and HL.

Read more »

How To Prove Congruent Triangles In A Rectangle

Given is the midpoint of CD. - Show that both pairs of opposite sides are congruent.

Congruent Triangles Methods Of Proving Triangles Congruent Missing Statements Proof Practice Packe Proving Triangles Congruent Secondary Math Teacher Resources

So the area of the rectangle is base height.

How to prove congruent triangles in a rectangle. To prove that the diagonals are congruent you will first want to prove that. Here is what is given. The diagonals of a parallelogram bisect each other.

ABCD is a rectangle and Complete the following proof. If a parallelogram is a rectangle then its diagonals are congruent. Prove that the diagonals of a rectangle are congruent.

If you flipreflect MNO over NO it is the same as ABC so these two triangles are congruent. - Show that one pair of sides is parallel and congruent. AB DC Opposite sides of rectangle BC AD Opposite sides of rectangle AC C A Common side ABC C AD By S S S congruence property.

Here is what you need to prove. As you can hopefully see both diagonals equal 13 and the diagonals will always be congruent because the opposite sides of a rectangle are congruent allowing any rectangle to be divided along the diagonals into two triangles that have a congruent hypotenuse. Click to see full answer.

If the length divided by the width is rational then yes. A 3 1 B 4 5 C 2 3 D -1 -3 E -5 -4 F -3 -2 a The triangle are congruent because triangle ABC can be mapped to triangle DEF by a rotation. Draw a rectangle with its diagonals and preview the proof.

These are two right triangles and their hypotenuses are the diagonals of the rectangle. ABCD is a rectangle and Q 1. A good way of reasoning about this problem abstractly would be to observe that the triangles are both right triangles and the lengths of the sides that come together to form the right angles are 4 and 8 units respectively.

If one angle is right then all angles are right. Segment AC segment BD. Opposite angels are congruent D B.

Just partition the rectangle into congruent squares and cut each square along a diagonal. So if you have two triangles and you can transform for example by reflection one of them into the other while preserving the scale the two triangles are congruent. Opposite sides are congruent AB DC.

Prove that the triangles with the given vertices are congruent. There are 5 different ways to prove that this shape is a parallelogram. The first way to prove that the diagonals of a rectangle are congruent is to show that triangle ABC is congruent to triangle DCB.

Again we can use the Pythagorean theorem to find the hypotenuse NL. Basically triangles are congruent when they have the same shape and size. Each diagonal of a parallelogram separates it into two congruent triangles.

Why do we assume the to congruent triangles have the same area And you prove that a parallelogram has the area base times height because if you cut of a right triangle from one side to and move it to the other you have a rectangle that has sides that are length base and length height. Consecutive angles are supplementary A D 180. In ABC and C AD.

So to show that they are congruent we just need to align the right angles and the sides with corresponding lengths. - Show that both pairs of opposite sides are parallel. Since ABCD is a rectangle it is also a parallelogram.

Choose one of the methods.

Read more »

Which Is A Congruence Statement For The Pair Of Triangles Represented By

Two triangles are congruent if their corresponding sides are equal in length and their corresponding interior angles are equal in measure. Two equal angles and a side that does not lie between the two angles prove that a pair of triangles are congruent by the AAS Postulate Angle Angle Side.

Pin On Tpt Math Lessons

4 WVU GHI W V U G H I W.

Which is a congruence statement for the pair of triangles represented by. SAS and SSS are what we can use to justify triangle congruence. Two triangles are said to be congruent if one can be placed over the other so that they coincide fit together. We go through three examples discussing techni.

XY CA XZ CB ZXZC 11. ΔJMK ΔLKM by SAS or ASA J K L M Ex 7 Determine if whether each. Determine whether each pair of triangles is congruent.

Which statement about the triangles is true. ASA angle angle side congruence theorem. 5 ZXY ZXC Y X Z C Y.

Corresponding sides and angles mean that the side on one triangle and the side. Congruent Triangles Triangles that have exactly the same size and shape are called congruent triangles. GH RT GI RS HI TS Determine Whether Each Pair Of Triangles Is Congruent.

6 DEF DSR E F D R S F. This means that congruent triangles are exact copies of each other and when fitted together the sides and angles which coincide called corresponding sides and angles are equal. Name a pair of overlapping congruent triangles in each diagram.

ASA Postulate angle side angle When two angles and a side between the two angles are equal for 22 triangles they are said to be congruent by the ASA postulate Angle Side Angle. If So Write A Congruence Statement And Explain Why The Triangles Are Congruent. 1 DEF KJI D E F K J I FD.

1 A B C is congruent to D E F. CB EF CA ED BA FD 10. We use the symbol to show congruence.

For instance LA L F AB FG LB L G BC GH Also recall that the congruence patterns for triangles ASA. 17. 3 TUV GFE T U V F G E U.

So the triangles are congruent by Hypotenuse -Angle HA congruence theorem. Open-Ended Draw two parallel lines and draw two parallel transversals through your parallel lines. If in two right triangles the hypotenuse and one leg of one are congruent to the hypotenuse and one leg of the other then the two triangles are congruent.

In the case of right triangles this is known as the Hypotenuse Leg Congruence Theorem. The triangles can be proven congruent by SAS. We can show by counterexample that for non-right triangles SSA congruence may not be sufficient for triangle congruence.

Congruence and Triangles Complete each congruence statement by naming the corresponding angle or side. Which statement indicates that the triangles in each pair are congruent. 16.

2 BAC LMN B A C M L N A. Label your triangles and write. ΔACB ΔECD by SAS B A C E D Ex 6 Determine if whether each pair of triangles is congruent by SSS SAS ASA or AAS.

The triangles can be proven congruent by SSS. 9th - 12th grade. The triangles can be proven congruent by SSA.

Learn how to write a triangle congruence statement in this free math video tutorial by Marios Math Tutoring. Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle. If so write a congruence statement and explain why the triangles are congruent.

The symbol for congruent is. Then draw a third transversal to create two congruent triangles. Complete the congruence statement.

The hypotenuses and a pair of corresponding angles of the right triangles are congruent. State whether the triangles are congruent by SSS SASASAAAS or HL. If it is not possible to prove that they are congruent write not possible.

9th - 12th grade. Remember that when you write a congruence statement such as AABC AFGH the corresponding parts of the two triangles must be the parts that are congruent. This concept teaches students how to write congruence statements and use congruence statements to determine the corresponding parts of triangles.

If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle then the two triangles are congruent. Gruent each pair of corresponding sides are congruent and each pair of corre- sponding angles are congruentWe use three pairs of corresponding parts SAS ASA or.

Read more »

What Is A Congruence Statement For The Pair Of Triangles

If so write a congruence statement and explain why the triangles are congruent. JK MN LK ON ZK ZN 9.

Pin On Tpt Math Lessons

LA leg-acute angle Congruence Theorem.

What is a congruence statement for the pair of triangles. Congruence of Triangles Congruence of triangles. We have MAC and CHZ with side m congruent to side c. You have to be careful when writing the congruence statement because the letters of one.

The symbol for congruent is. The term congruent in geometry indicates that two objects have the same dimensions and shape. When you have a right triangle and the hypotenuses are congruent and the legs are congruent then you can say that the two triangles are also congruent.

Write the congruence statement for each pair of congruent triangles. GH RT GI RS HI TS Determine whether each pair of triangles is congruent. By the ASA Postulate these two triangles are congruent.

Triangles that have exactly the same size and shape are called congruent triangles. 001854 Write a congruence statement for the pair of congruent figures Examples 5-6 002730 Find x and y given pair of congruent quadrilaterals Example 7 003104 Find x and y given pair of congruent triangles Example 8 003343 Give the reason for each statement Example 9 Practice Problems with Step-by-Step Solutions. How do you prove triangle congruence.

Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle. Complete the congruence statement for each pair of triangles. Although congruence statements are often used to compare triangles they are also used for lines circles and other polygons.

Write a congruence statement for each pair of triangles represented. Congruence is defined as agreement or harmony. In this blog we will understand how to use the properties of triangles to prove congruency between 22 or more separate triangles.

If a leg and an acute angle of one right triangle are congruent to a leg and an acute angle of another right triangle then the triangles are congruent. Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. Congruence Statements Corresponding angles and sides of congruent triangles are congruent.

Roberto proved that they are congruent using AAS. If two angles and the included side of a triangle are congruent to two angles and the included side of another triangle then the two triangles are congruent. A is congruent to H while C is congruent to Z.

These triangles can be slides rotated flipped and turned to be looked identical. The triangles in Figure 1 are congruent triangles. Note that when writing congruency statements the order of the letters is critical as each angleside in the first triangle must be congruent to its corresponding angleside in the second triangle.

Two triangles are said to be congruent if one can be superimposed on the other such that each vertex and each side lie exactly on top of the other. 1 D ABC 2 D UVW 3 D PQR 4 D KLM 5 D DEF 6 D TUV 7 D DEF D STR D XYZ D JKL D NML. AAS is equivalent to an ASA condition by the fact that if any two angles are given so is the third angle since their sum should be 180.

If the legs of one right triangle are congruent to the legs of another right triangle then the triangles are congruent. Two triangles are said to be congruent if one can be placed over the other so that they coincide fit together. When triangles are congruent it means that they have the same size sides and the same angle measures.

Nessa proved that these triangles are congruent using ASA. Hope this helps. Which statement and reason would be included in Robertos proof that was not included in Nessas proof.

If two pairs of angles of two triangles are equal in measurement and a pair of corresponding non-included sides are equal in length then the triangles are congruent. For example a congruence between two triangles ABC and DEF means that the three sides and the three angles of both triangles are congruent. ΔABP is congruent to ΔBAQ.

CB EF CA ED BA FD 10. XY CA XZ CB ZXZC 11. Based on the above the congruency statement would be.

P 23 We M 23 N. Get some practice identifying corresponding sides. This means that congruent triangles are exact copies of each other and when fitted together the sides and angles which coincide called corresponding sides and angles are equal.

When you have two congruent figures that means that corresponding sides and corresponding angles are congruent.

Read more »

What Are The Properties Of Congruent Triangles

Triangles that have exactly the same size and shape are called congruent triangles. Two triangles are said to be congruent if one can be superimposed on the other such that each vertex and each side lie exactly on top of the other.

Prove Triangles Similar Via Aa Sss And Sas Similarity Theorems Notes Are More Fun When Doodling Mathematics Worksheets Doodle Notes Notes

А А 1.

What are the properties of congruent triangles. The diagonals are congruent and bisect each other divide each other equally. On the other hand triangles that are not congruent are called non-congruent triangles. Congruence is defined as agreement or harmony.

Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. Properties of a Rectangle Opposite sides are parallel and congruent. Basic properties of triangles The sum of the angles in a triangle is 180.

Congruent Triangles Section 4-4. If ΔАВС ΔА 1 В 1 С 1 then. In this blog we will understand how to use the properties of triangles to prove congruency between 22 or more separate triangles.

This is called the angle-sum property. This is the very first criterion of congruence. All angles are right.

The sum of the lengths of any two sides of. These triangles can be slides rotated flipped and turned to be looked identical. But you dont need to know all of them to show that two triangles are congruent.

These properties can be applied to segment angles triangles or any other shape. There are three very useful theorems that connect equality and congruence. Use the SSS Postulate to test for triangle congruence Use the SAS Postulate to test for triangle congruence.

Two angles are congruent if and only if they have equal measures. The first property of congruent triangles In congruent triangles their respective elements are congruent this follows from the definition of the congruence of triangles. SSS Criterion for Congruence SAS Criterion for Congruence ASA Criterion for Congruence AAS Criterion for Congruence RHS Criterion for Congruence.

If you flipreflect MNO over NO it is the same as ABC so these two triangles are congruent. Any triangle is defined by six measures three sides three angles. If there is a rigid transformation which maps to this means that In other words corresponding parts of congruent triangles are congruent.

The symbol for congruent is. The properties of congruent triangles are. If repositioned they coincide with each other.

The fundamental property of rigid motions of the plane is that they do not change angle measurements or side lengths. The symbol between the triangles indicates that the triangles are congruent. Two triangles are congruent if and only if all corresponding angles and sides are congruent.

Triangles to be congruent they should have two equal sides and one equal angle comprising the same sides. Two segments are congruent if and only if they have equal measures. The triangles in Figure 1 are congruent triangles.

Congruent triangles are triangles having all three sides of exactly the same length and all three angles of exactly the same measure. The meaning of the reflexive property of congruence is that a segment an angle a triangle or any other. The symbol of congruence is.

Reflexive property of congruence. So if you have two triangles and you can transform for example by reflection one of them into the other while preserving the scale the two triangles are congruent. SSSside side side SAS side angle side ASA angle side angle AAS angle angle side HL hypotenuse leg of a right triangle.

Proving Congruence SSS and SAS SOL. A triangle is said to be congruent to. G5 The student will b prove two triangles are congruent or similar given information in the form of a figure or statement using algebraic and coordinate as well as deductive proofs.

We know angle A. The three properties of congruence are the reflexive property of congruence the symmetric property of congruence and the transitive property of congruence. When two shapes sides or angles are congruent well use the symbol above.

The figure below will make things clear. Thus congruent triangles are mirror image of each other. SAS Congruence Rule SAS stands for Side-Angle-Side.

Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle. Basically triangles are congruent when they have the same shape and size.

Read more »

How To Prove Two Triangles In A Rectangle Are Congruent

Two or more triangles are said to be congruent if they have the same shape and size. Conclude that A C D is congruent to C A B.

Triangles Triangle Congruence Practice Sss Sas Asa Aas Hl 20 Task Teacher Tools Task Cards Task

We discussed today the concepts about Proving Two Triangles are Congruent.

How to prove two triangles in a rectangle are congruent. Two or more triangles are said to be congruent if they have the same shape and size. There are many p. Because they both have a right angle.

- Show that both pairs of opposite sides are parallel. Each diagonal of a parallelogram separates it into two congruent triangles. The second way to prove that the diagonals of a rectangle are congruent is to show that triangle ABD is congruent to triangle DCA Here is what is given.

- Show that both pairs of opposite sides are congruent. There are several different postulates you can use to prove that two triangles are congruent - that they are exactly the same size and shape. I hope youll learn somethi.

Segment AC segment BD. There are 5 different ways to prove that this shape is a parallelogram. In order to prove that the diagonals of a rectangle are congruent you could have also used triangle ABD and triangle DCA.

Call A the image of point A under the rotation and C the image of point C. A Name four pairs of vertical angles. Rectangle ABCD Here is what you need to prove.

- Show that one pair of sides is parallel and congruent. Two triangles can be proved similar by the angle-angle theorem which states. _____ Unit 8 Day 3 - Proving Triangles Congruent Classwork 1.

Click to see full answer. A 0 0 D a 0 B b 0 because AD AE so E acosθ asinθ. Draw the image of triangle A C D when it is rotated 180 about vertex D.

E is a point on the line AC so we can propose a coefficient λ that satisfies AC λ AE and 0 λ 1 then C λacosθ λasinθ. Show that A C D can be translated to C A B. Learn how to prove that two triangles are congruent.

The congruence postulates covered in this lesson are Side-Side-Side SSS Side-Angle-Side SAS Angle-Side-Angle ASA and Angle-Angle-Side AAS. Learn how to prove that two triangles are congruent. This theorem is also called the angle-angle-angle AAA theorem because if two angles of the triangle are congruent the third angle must also be congruent.

I AB AC Hypotenuse ii AD AD Common side Leg Hence the two triangles ABD and ACD are congruent by Hypotenuse-Leg HL theorem. Choose one of the methods. 8 7 6 5 4 3 2 1 Name.

Consecutive angles are supplementary A D 180. If one angle is right then all angles are right. If two triangles have two congruent angles then those triangles are similar.

Sometimes when you are trying to decide if triangles are congruent you need to identify other sides or angles that are congruent. Opposite angels are congruent D B. I Triangle ABD and triangle ACD are right triangles.

The diagonals of a parallelogram bisect each other. 3 months ago SAS stands for side angle side and means that we have two triangles where we know two sides and the included angle are equal. Explain why D A D A and why D C is parallel to A B.

B Name four pairs of corresponding angles. Its me again Mark ChavezWelcome to my latest vlog. If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle the triangles are congruent.

We do it by using the coordinate system like the picture. There are many p.

Read more »

How To Prove Congruent Triangles Examples

AAS Postulate angle angle side Two equal angles and a side that does not lie between the two angles prove that a pair of triangles are congruent by the AAS Postulate Angle Angle Side. Sometimes when you are trying to decide if triangles are congruent you need to identify other sides or angles that are congruent.

Geo Chapter 4 Lesson 2 Homework Congruent Triangle Theorems Geometry Worksheets Congruent Triangles Worksheet Math Geometry

Two triangles ABC and PQR are such that.

How to prove congruent triangles examples. Learn how to use the Triangle Proportionality Theorem to complete triangle proportions solve word problems and find the value of the missing sides of a triangle. Below is the proof that two triangles are congruent by Side Angle Side. Triangle Congruence Theorems file name.

AB 35 cm BC 71 cm AC 5 cm PQ 71 cm QR 5 cm and PR 35 cm. Complete videos list. When triangles are congruent all pairs of corresponding sides are congruent and all pairs of corresponding angles are congruent.

In Step 1 Sal stated that angles AEB and DEC are congruent because they are vertical angles. Check whether the triangles are congruent. Examples solutions videos and lessons to help High School students learn how to use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures.

SideSide-Side SSS If AB EF BC FG AC EG then ΔABC ΔEFG. Congruent by what we abreviate to be CPCTC which means Corresponding Parts of Congruent Triangles are Congruent. A Name four pairs of vertical angles.

Triangle ABC and PQR are congruent ABC PQR if length BAC PRQ ACB PQR. 8 7 6 5 4 3 2 1 Name. Proving that a point is the midpoint via triangle congruencyWatch the next lesson.

SideAngleSide SAS If AB EF BAC FEG AC EG then ΔABC ΔEFG. Fortunately it is not necessary to show all six of these facts to prove triangle congruence. If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle then the two right triangles are congruent.

In the right triangles ΔABC and ΔPQR if AB PR AC QR then ΔABC ΔRPQ. Vertical angles are angles that across from each other and made by two intersecting lines and they are ALWAYS congruent. HSG-SRTB5 CPCTC is an acronym for Corresponding Parts of Congruent Triangles are Congruent.

In the example of the frame of an umbrella at the right we can prove the two triangles congruent by SAS. Worked examples of triangle congruence. Can you imagine or draw on a piece of paper two triangles B C A X C Y whose diagram would be consistent with the Side Angle Side proof shown below.

The five ways of identifying congruent triangles are shown below. Figure 4 Heading. This article includes the Triangle Proportionality Theorem proof and examples that can help you fully gauge your understanding of it.

Again you have to prove the two triangle congruent before you can ever use CPCTC. AB PR 35 cm. B Name four pairs of corresponding angles.

The Hypotenuse-Leg HL Rule states that. _____ Unit 8 Day 3 - Proving Triangles Congruent Classwork 1. Proving Triangles Congruence Rules Theorems.

If two triangles have one angle equal and two sides on either side of the angle equal the triangles are congruent by SAS Postulate Side Angle Side. There are five ordered combinations of these six facts that can be used to prove triangles congruent.

Read more »

How To Find The Value Of Congruent Triangles

Two figure are congruent if both have the same shape. Two triangles ABC and ABC are similar if and only if corresponding angles have the same measure.

Corresponding Sides And Angles Of Congruent Triangles Worksheet 7 G 1 Congruent Triangles Worksheet Triangle Worksheet Trigonometry Worksheets

The top and bottom faces of a kaleidoscope are congruent.

How to find the value of congruent triangles. The LaTex symbol for congruence is cong written as cong. In Euclidean geometry any three points when non-collinear determine a unique triangle and simultaneously a unique plane ie. Note that for congruent triangles the sides refer to having the exact same length.

What is the value of x in this equation. It can be shown that two triangles having congruent angles equiangular triangles are similar that is the corresponding sides can be proved to be proportional. If you rotate or flip the page it will remain the same as the original page.

In the figure PQR and SQR are two right triangles with common hypotenuse QR. Identifying Additional Congruent Parts A. In this first problem over here were asked to find out the length of this segment segment seee and we have these two parallel lines a B is parallel to de and then we have these two essentially transversals that form these two triangles so lets see what we can do here so the first thing that might jump out at you is that this angle and this angle are vertical angles so they are going to be.

If two triangles are congruent then each part of the triangle side or angle is congruent to the corresponding part in the other triangle. If not say no. The triangles are congruent by the SSS congruence theorem.

Properties of Congruent Triangles. Class 7 Maths Congruence of Triangles TrueT And FalseF 1. We have the methods of SSS side-side-side SAS side-angle-side and ASA angle-side-angle.

This is the true value of the concept. A two-dimensional Euclidean spaceIn other words there is only one plane that contains that triangle and every. 8x 40 180 Use the z-distribution table on pages A-1 and A-2 or technology to solve.

Congruent Triangles Explanation Examples. Two triangles are congruent if they have the same three sides and exactly the same three angles. Find the length of each altitude of an equilateral triangle Solution.

Determine if you can use SSS SAS ASA AAS and HL to prove triangles congruent. A triangle is a polygon with three edges and three verticesIt is one of the basic shapes in geometryA triangle with vertices A B and C is denoted. If three corresponding angles of two triangles are equal then triangles are congruent.

Once you have proved two triangles are congruent you can find the angles or sides of one of them from the other. The congruent figure super impose each other completely. You must be well aware of the photocopy machine.

Suppose a set of data is normally distributed. Which rigid transformations can map MNP onto TSR Get the answers you need now. If PR and SQ intersect at M such that PM 3 cm MR 6 cm and SM 4 cm find the length of MQ.

When you put an A4 page inside the machine and activate it you get an identical copy of that page. This implies that they are similar if and only if the lengths of corresponding sides are proportional.

Read more »

Methods To Identify Congruent Triangles Worksheet Answers

In this congruent triangles worksheet students identify congruent triangles using the hypotenuse-leg congruence theorem. Printable in convenient PDF format.

Proving Triangles Congruent With Congruence Shortcuts Proving Triangles Congruent Geometry Lessons Teaching Geometry

1 A ASA B AAS C Not congruent D SSS 2 A AAS B SSS C ASA D Not congruent 3 A SSS B ASA C Not congruent D AAS 4 A Not congruent B ASA C AAS D SAS 5 A Not congruent B ASA C SSS D AAS 6 A ASA B SAS C AAS D SSS 7.

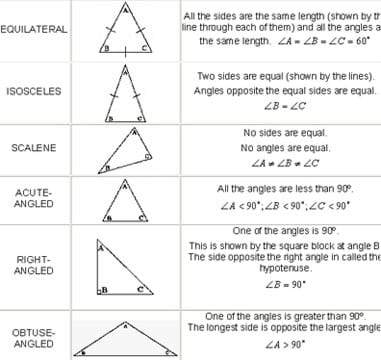
Methods to identify congruent triangles worksheet answers. Video for Lesson 4-5. They determine the length of a missing side and write proofs to determine congruence of triangles. Use the triangle congruence criteria sss sas asa and aas to determine that two triangles are congruent.

Answer key is included. Video for Lesson 4-4. Observe the congruent parts keenly and write the statement in the correct order.

Practice worksheet for lesson 4-2. Teacher guide Identifying Similar Triangles T-1 Identifying Similar Triangles MATHEMATICAL GOALS This lesson unit is intended to help you assess how students reason about geometry and in particular how well they are able to. Indicate the Congruent Angles and Sides.

If the triangles cannot be proven congruent state not possible. Side side side is a rule used to prove whether a. Circle the letters beneath the correct method in the chart to.

Triangle Congruence Proofs - CPCTC - Corresponding Parts. State if the two triangles are congruent. A F 21.

Identifying solid figures Volume of prisms and cylinders. 21 a sss b sas c asa d aas 22 a aas b sas c sss d not congruent 23 a sas b aas. If they are state how you know.

AABC AEFD B 21. Worksheet Geometry Answer Key. AACB AADB D 23.

Subtract 126 from both sides. Use the given information to mark the diagram appropriately. Feb 9 2017 - Five Methods for Proving Triangles Congruent Riddle Practice Worksheet This riddle practice worksheet allows students to practice determining whether a pair of triangles are congruent or not.

Free Geometry worksheets created with Infinite Geometry. 126 C 180. Name the triangle congruence pay attention to proper correspondence when naming the triangles and then identify the Theorem or Postulate SSS SAS ASA AAS HL that would be used to prove the triangles congruent.

Practice worksheet for lesson 4 4. Congruent Triangles Geometry chapter 4 triangle congruence proofs answers. Practice worksheet for lesson 4-4.

By Third Angle Theorem the third pair of angles must also be congruent. Concepts and Applications Geometry chapter 4 triangle congruence proofs answers. AAIC ACDA ABDC ACDE LMQP.

Write congruence statement for each pair of triangles in this set of congruent triangles worksheets. State if the two triangles are congruent. Because they both have a right angle.

E C 54. Lesson 4-3 Proofs for congruent triangles. Other Methods of Proving.

Write the Congruence Statement. Other methods of proving. In triangles ABC and DEF we have.

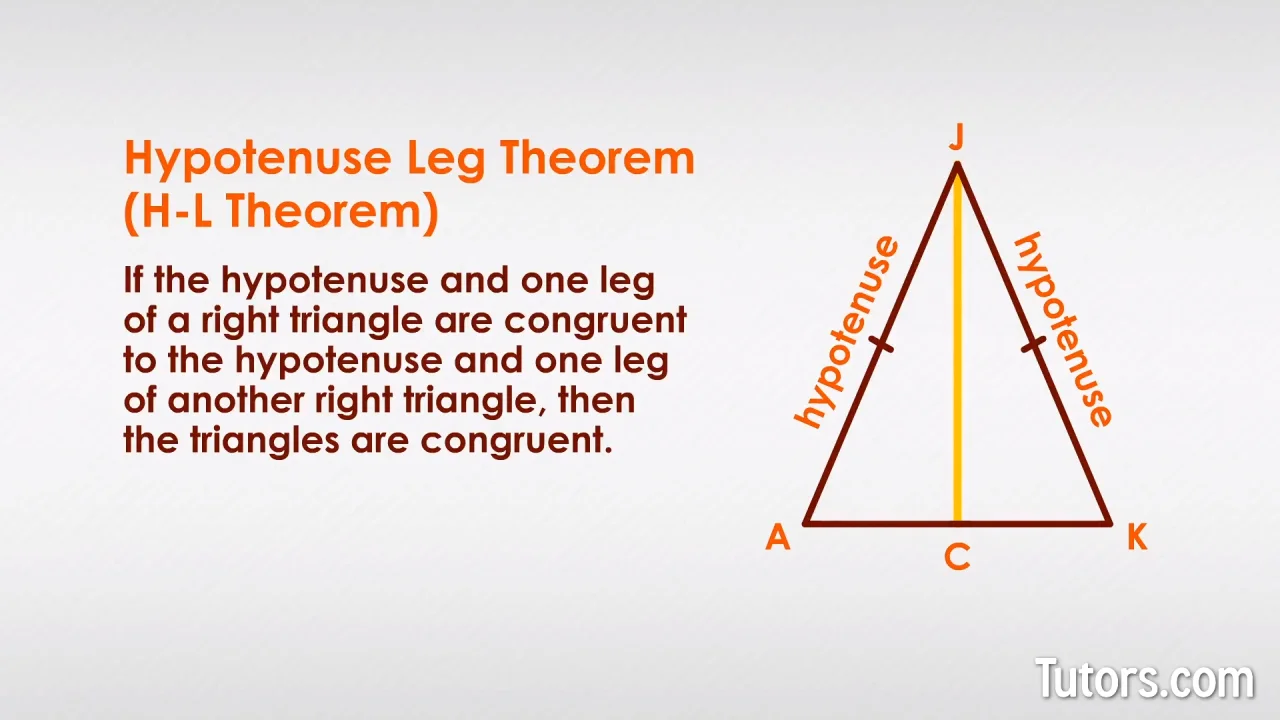
Answer key for 4-2 practice worksheet. Congruent Triangles Classifying triangles Triangle angle sum The Exterior Angle Theorem Triangles and congruence SSS and SAS congruence ASA and AAS congruence. Ii PR WX Leg Hence the two triangles PQR and WXY are congruent by Hypotenuse-Leg theorem.

Triangle congruence worksheet 1 answer key or congruent triangles worksheet grade 7 kidz activities. Geometry Worksheet Congruent Triangles NAME Date HR a Determine whether the following triangles are congruent- b If they are name the triangle congruence pay attention to proper correspondence when naming the triangles and then identify the Theorem or Postulate SSS SAS ASA AAS HI that supports your conclusions c Be sure to show any additional congruence. Answer key for 4-4 practice worksheet.

The Isoceles Triangle Theorems. I Triangle PQR and triangle WXY are right triangles. ASA angles and side of one triangle are congruent to 2 angles and the included side of another triangle.

Geometry worksheet congruent triangles sss and sas answers. Triangle Congruence Worksheet 1 For each pair of triangles tell which postulates if any make the triangles congruent. I PQ XY Hypotenuse.

1 Not congruent 2 ASA 3 SSS 4 ASA 5 Not congruent 6 ASA 7 Not congruent 8 SSS 9 SAS 10 SSS-1-. If they are congruent they need to give the method that can be. Use the diagrams and the information given to determine which of the above methods will prove the triangles congruent.

21 105 C 180. If three sides of one triangle are equal to three sides of another triangle then the triangles are congruent. Use facts about the angle sum and exterior angles of triangles.

This worksheet contains proofs and problems where students must show that sides or angles are congruent using the triangle congruence postulates SSS SAS ASA AAS and CPCTC Congruent Parts of. Two angles of one triangle are congruent to two angles of another triangle. 4-7 Triangles and Coordinate Proof.

Notes for lesson 4-4. Virginia SOLs Geometry Correlated to Glencoes Geometry and Geometry. C 54.

Proving triangles congruent worksheet answers. If they are state how you know. Sides and the included angle of another triangle.

Check whether two triangles PQR and WXY are congruent.

Read more »

What Is Rhs In Congruent Triangles

Congruent triangles are triangles that have the same size and shape. Side Angle SideSide Side SideAngle Side AngleAngle Angle SideThats an easy way to memorize the reasons of congruent triangles.

Math Infographics Tentors Math Teacher Resources Online Education Math Resources Math

There exist three rigid motions.

What is rhs in congruent triangles. In RHS congruence criteria Both triangle will have a right angle. SSS SAS ASA AAS RHS. RHS congruence theorem states that if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle the two triangles are congruent.

A right angle the hypotenuse. Anyone of other two sides of both triangle are equal. In this article we will discuss two important criteria for congruence of triangles RHS Right angle Hypotenuse Side and SSS Side Side Side.

If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle then the two right triangles are said to be congruent by RHS rule. RHS Congruence Rule Theorem. It is easy enough to prove it works simply use Pythagorus theorem to reduce to SSS.

RHS rule Congruence of right angled triangle illustrates that if hypotenuse and one side of right angled triangle are equal to the corresponding hypotenuse and one side of another right angled triangle. When two angles and a side between the two angles are equal for 22 triangles they are said to be congruent by the ASA postulate Angle Side Angle. And a corresponding side are equal RHS right angle hypotenuse side.

RHS Postulate Right Angle Hypotenuse Side The RHS postulate Right Angle Hypotenuse Side applies only to Right-Angled Triangles. RHS is a well known test for determining the congruency of triangles. Then both the right angled triangle are.

In two right-angled triangles if the length of the hypotenuse and one side of one triangle is equal to the length of the hypotenuse and corresponding side of the other triangle then the two triangles are congruent. Two triangles are congruent if two pairs of corresponding angles and a pair of corresponding sides are equal. Two right-angled triangles are congruent if the hypotenuses and one pair of corresponding sides are equal.

If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle then the two triangles are congruent. The following diagrams give the rules to determine congruent triangles. This means that the corresponding sides are equal and the corresponding angles are equal.

Two geometrical figures not only triangles are congruent if they can be brought to coincide by applying on one of them any combination of rigid motions. Rigid motions are movements of a figure in space such that both the shape and the size of the figure is maintained. I thought that it seems strange that this only works for an angle being 90 degrees - or does it.

Scroll down the page for examples and solutions. The right angle-hypotenuse-side RHS principle. To prove two triangles congruent We use RHS criteria when.

Theorem 75 RHS congruence rule - If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle then the two triangle are congruent. RHS criterion of congruence stands for Right Angle-Hypotenuse-Side full form of RHS congruence. S ide are equal.

Hypotenuse of both triangles are equal. RHS Rule of Congruent Triangles.

Read more »

Congruent Triangles Sss Sas Asa Aas Hl Worksheet Answers

SSS stands for side side side and means that we have two triangles with all three sides equal. Geometry worksheet congruent triangles asa and aas answers from triangle congruence worksheet 1 answer key source.

Pin On Geom Congruent Triangles

Asa aas and hl practice a 1.

Congruent triangles sss sas asa aas hl worksheet answers. 1 1 A 2 D 3 C 4 A. This activity includes three parts that can be done all in one lesson or spread out across a unit on congruent triangles. Links Videos demonstrations for proving triangles congruent including ASA SSA ASA SSS and Hyp-Leg theorems.

1 HL 2 SSS 3 AAS 4 Not congruent 5 ASA 6 SSS 7 SAS 8 SAS 9 AAS-1-. Triangle Congruence Oh My Worksheet - Math Teacher Mambo November 2010. The quiz will assess your understanding of concepts.

The SSS rule states that. These congruent triangles notes and worksheets covercongruent triangle introcongruent shortcuts sss sas asa aas hlcongruent triangle measures with algebraproofs with and without cpctceach topic includes at least one practice worksheet. You will need a separate piece of paper to show all your work.

SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal. There are five ways to find if two triangles are congruent. A X B C Y Z.

SSS SAS ASA AAS and HL. Answers to Assignment ID. Improve your math knowledge with free questions in Proving triangles congruent by SSS SAS ASA and AAS and thousands of other math skills.

Side-Side-Side is a rule used to prove whether a given set of triangles are congruent. State if the two triangles are congruent. Sss and sas of another triangle then the triangles are congruent.

The origin of the word congruent is from the Latin word congruere meaning correspond with or in harmony. Asa and aas theorems. Triangle Congruence a Determine whether the following triangles are congruent b If they are name the triangle congruence pay attention to proper correspondence when naming the triangles and then identify the Theorem or Postulate SSS SAS ASA AAS HL that supports your conclusion.

Share skill IXL - SSS SAS ASA and AAS Theorems Geometry practice There are five ways to find if two triangles are congruent. Name the postulate if possible that makes the triangles congruent. If three sides of one triangle are equal to three sides of another triangle then the triangles are congruent.

Congruent Triangles Sss And Sas Worksheet Answers Nidecmege. I can prove triangles are congruent using SSS ASA. Hl Triangle Congruence Worksheet Answers.

Sas Sss Asa Aas And Hl. State what additional information is required in order to know that the triangles are congruent for the reason given. Hypotenuse- Leg HL Congruence Theorem.

If they are state how you know. Congruent Triangles by SSS SAS ASA AAS and HL - practice review activity set for triangle congruence with shortcuts. If you slid triangle a to the right it would exactly answer.

SSS ASASAS AAS and HL State if the two triangles are congruent. A collection of congruent triangles worksheets on key concepts like congruent parts of congruent triangles congruence statement identifying the postulates congruence in right triangles and a lot more is featured here for the exclusive use of 8th grade and high school students. Triangle congruence online worksheet for 9.

11 ASA S U T D 12 SAS W X V K 13 SAS B A C K J L 14 ASA D E F J K L 15 SAS H I J R S T 16 ASA M L K S T U 17 SSS R S Q D 18 SAS W U V M K-2-. A sample problem is students will prove the congruence of each pair of triangles. Play this game to review Geometry.

If they are state how you know. SSS SAS ASA AAS and HL. In the diagrams below if AB RP BC PQ and CA QR then triangle ABC is congruent to triangle RPQ.

Geometry K5 SSS SAS ASA and AAS Theorems LER. The diagonal is the hypotenuse of an isosceles right triangle. Worksheet template 4 6 using congruent triangles cpctc from triangle congruence worksheet answers source.

You can print the two sets of Triangle Cards for worksheets A and C on colored cardstock if desired. 234 3-11 19 22-25 31 15 problems Triangle Congruence Worksheet 1 Friday 11912. 1 A SSS B SAS C AAS D Not congruent 2 A AAS B SAS.

ASA AAS and HL I can prove triangles are congruent using ASA AAS and HL I can mark pieces of a triangle congruent given how they are to be proved. If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and leg of a second right triangle then the two triangles are congruent. If three sides of one triangle are equal to three sides of another triangle the triangles are congruent.

SSS side side side. 21 A SSS B ASA C AAS D SAS 22 A AAS B SAS C ASA D Not congruent.

Read more »