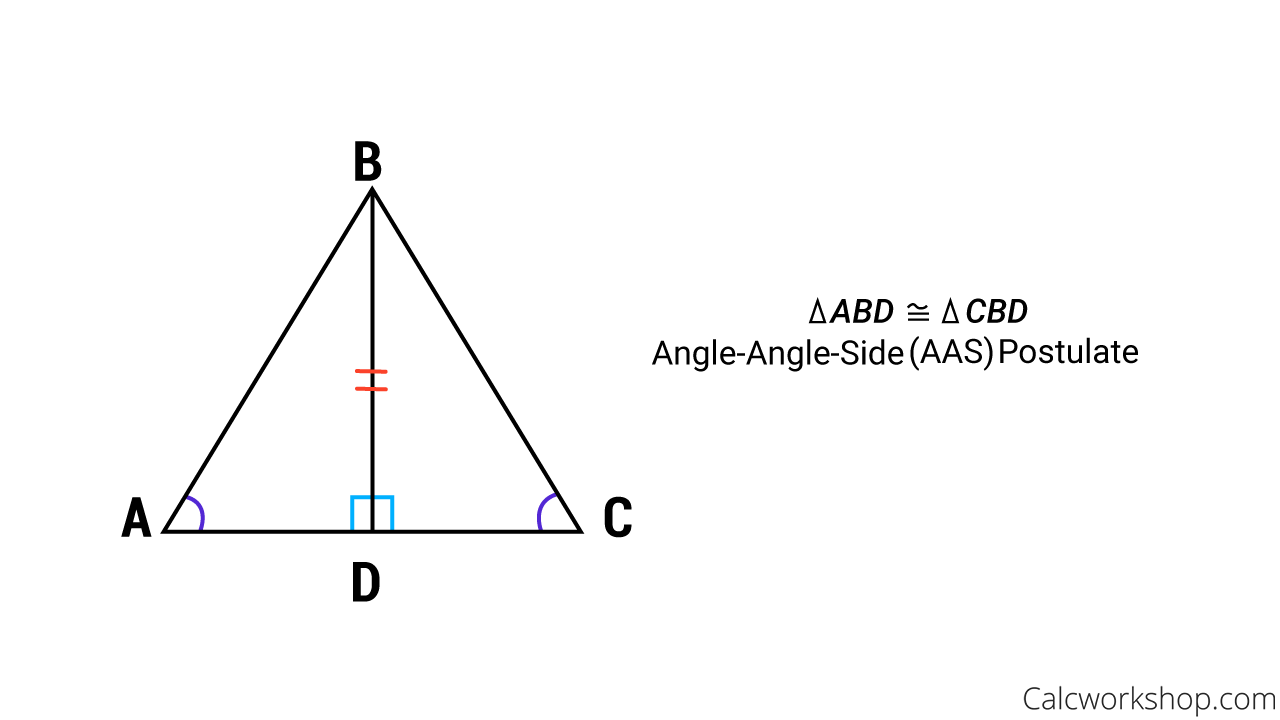Practice Proving Triangles Congruent Asa Aas

Sss All three sides are congruent. Write that name in order on the lines for the problem number see box at bottom.

Congruent Triangles Methods Of Proving Triangles Congruent Missing Statements Proof Practice Packe Proving Triangles Congruent Secondary Math Teacher Resources

Use the triangle congruence criteria SSS SAS ASA and AAS to determine that two triangles are congruent.

Practice proving triangles congruent asa aas. Δ JMK Δ LKM by SAS or ASA J K L M Ex 7 28. Label the endpoints A and B. If Angle A D Side AC Æ DF Æ and Angle C F then ABC DEF.

11 ASA S U T D 12 SAS W X V K 13 SAS B A C K J L 14 ASA D E F J K L 15 SAS H I J R S T 16 ASA M L K S T U 17 SSS R S Q D 18 SAS W U V M K-2-. ASA and AAS 1 Draw a segment 3 inches long. Triangle are congruent to two angles and the included side of a second triangle then the two triangles are congruent.

If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non included side of a second triangle then the triangles are congruent. Key Words vertical angles p. State what additional information is required in order to know that the triangles are congruent for the reason given.

AD CD LA E LCJ g. Angle-AngleSide Congruence Theorem If two angles and a non-included side of one triangle are congruent to two angles and the corresponding nonincluded side of a second triangle then the triangles are congruent. If it is not possible to prove that they are congruent write not possible.

Determine if whether each pair of triangles is congruent by SSS SAS ASA or AAS. Also indicate which postulate or theorem is being used. ASA AAS SAS SSS date.

B A Y X. Proving Triangles Congruent Asa Aas Sas Sss - Displaying top 8 worksheets found for this concept. Improve your math knowledge with free questions in Proving triangles congruent by ASA and AAS and thousands of other math skills.

Choose 5 key terms from this unit that you. SSS SAS HL right nsonly ASA AAS All three sides are congruent. AB CB bisects ZABC.

Δ ACB Δ ECD by SAS B A C E D Ex 6 27. For Your Notebook AAS Two angles and a non- included side are congruent. You have learned five methods for proving that triangles are congruent.

ADFG AFDE ZLGFD Chapter 4 12 CPC7C Glencoe Geometry. Some of the worksheets for this concept are 4 s sas asa and aas congruence 4 s and sas congruence Proving triangles are congruent by sas asa U niitt n 77 rriiaangllee g coonggruueenccee Unit 4 triangles part 1 geometry smart packet Proving triangles congruent Proving triangles congruent Triangle proofs s sas asa aas. If it is not possible to prove that they are congruent write not possible.

2 Draw an angle measuring 45 8 at point A. Geometry A Unit 6 Congruent Triangles I. Angle-Side-Angle ASA Postulate LDAC.

The congruent sides that are included between congruent angles are Write a congruence statement. Angle-side-angle is a rule used to prove whether a given set of triangles are congruent. Determine congruent triangles practice Khan Academy Use the triangle congruence criteria SSS SAS ASA and AAS to determine that two triangles are congruent.

DE Il FG ZE ZG Prove. Postulate 43 Postulate If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle then the two triangles are congruent. 11 ASA E C D Q 12 ASA K L M U S T 13 ASA R T S E C 14 ASA U W V M K 15 AAS E D C T 16 AAS Y X Z L M N 17 ASA G I V H 18 AAS J K L F-2-.

_____ For each problem give the correct naming order of the congruent triangles. Triangle Congruence Postulates and Theorems You have learned five methods for proving that triangles are congruent. SAS Two sides and the included angle are congruent.

75 alternate interior angles p. If two angles and the included side of one triangle are equal to two angles and included side of another triangle then the triangles are congruent. Two sides and the included angle are congruent.

Angle-Angle Side Congruence Theorem. HL right A only The hypotenuse and one of the legs are congruent. 250 Chapter 5 Congruent Triangles Goal Show triangles are congruent using ASA and AAS.

121 53 Proving Triangles are Congruent. The ASA rule states that. 3 Draw an angle measuring 30 8 at point B.

The hypotenuse and one of the legs are congruent. Identify congruent figures and corresponding parts of congruent figures Prove that two triangles are congruent using various methods such as SSS SAS ASA AAS and HL Prove that parts of two triangles are congruent Identify and use properties of isosceles and equilateral triangles II. Determine if whether each pair of triangles is congruent by SSS SAS ASA.

Determine if whether each pair of triangles is congruent by SSS SAS ASA or AAS. State what additional information is required in order to know that the triangles are congruent for the reason given. Improve your math knowledge with free questions in Proving triangles congruent by SSS SAS ASA and AAS and thousands of other math skills.

Skills Practice DATE PERIOD Proving Triangles CongruentASA AAS PROOF Write proor. THEOREM 45 Angle-Angle-Side AAS Congruence Theorem If two angles and a nonincluded side of one triangle are congruent to two angles and the. No other congruence relationships can be determined so ASA cannot be applied.

Read more »

Is Asa Always Congruent

Congruent Triangles - Two angles and included side ASA Definition. If two sides and the non-included angle of one triangle are congruent to two sides and the non-included angle of another triangle the two triangles are not always congruent.

Triangle Congruence Postulates Asa Aas Explained 2019

This can be used.

Is asa always congruent. Another shortcut is angle-angle-side AAS where two pairs of angles and the non-included side are known to. In the sketch below we have C A T and B U G. Thus we got two angles of one triangle is equal to the two angles of the next triangle then both triangles similar by AA similarity.

Suppose I made a movie which was. Forget math for a second. For a list see Congruent Triangles.

No SSA and SAS are two different things. The adjective congruent fits when two shapes are the same in shape and size. We have MAC and CHZ with side m congruent to side c.

ASS is not true in general. Speaking a little informally but still accurately mathmath means the exact same and mathequivmath means the same in all the important ways that matter. State what additional information is required in order to know that the triangles are congruent for the reason given.

So ASS doesnt work for all triangles on either the plane or a sphere or a hyperbolic plane. This is one of them ASA. This is because by those shortcuts SSS AAS ASA SAS two triangles may be congruent to each other if and only if they hold those properties true.

The Angle Side Angle Postulate ASA says triangles are congruent if any two angles and their included side are equal in the triangles. A is congruent to H while C is congruent to Z. Notice that C on C A T is congruent to B on B U G and A on C A T is congruent to U on B U G.

If two triangles are congruent all three corresponding sides are congruent and all three corresponding angles are congruent. By the ASA Postulate these two triangles are congruent. Triangles are congruent if any two angles and their included side are equal in both triangles.

If two pairs of corresponding angles and the side between them are known to be congruent the triangles are congruent. ASA works because there is one and only one triangle that can be drawn with specific angle side angle information. 11 ASA E C D Q 12 ASA K L M U S T 13 ASA R T S E C 14 ASA U W V M K 15 AAS E D C T 16 AAS Y X Z L M N 17 ASA G I V H 18 AAS J K L F-2-.

In the figure above AC DF BC EF AD but ABC is not congruent to DEF. An included side is the side between two angles. This shortcut is known as angle-side-angle ASA.

And similar triangles have corresponding angles equal thus the remaining third angle must be congruent therefore both the triangles are congruent by ASA postulate. The order of the letters matters a lot. Try this for yourself on these surfaces to see what happens.

Here the circle that has as its radius the second side of the triangle intersects the ray that goes from aalong the angle ato b twice. When all three sides are equal to each other on both triangles the triangle is congruent. If two sides and three angles of two triangles are congruent the triangles are congruent.

If two pairs of angles of two triangles are equal in measurement and a pair of corresponding non-included sides are equal in length then the triangles are congruent. There are five ways to test that two triangles are congruent. The ASA criterion for triangle congruence states that if two triangles have two pairs of congruent angles and the common side of the angles in one triangle is congruent to the corresponding side in the other triangle then the triangles are congruent.

ASA AAS SSS HL or SAS then all of their corresponding parts are congruent as well. Also vertical angles are always congruent. If any two angles and the included side are the same in both triangles then the triangles are congruent.

If two or more triangles are proven congruent by. If you lay two congruent triangles on each other they would match up exactlyCongruent comes from the Latin verb congruere to come together correspond with Figuratively the word. If two angles and the included side of a triangle are congruent to two angles and the included side of another triangle then the two triangles are congruent.

Read more »

How To Do Congruent Triangle Proofs

In this non-linear system users are free to take whatever path through the material best serves their needs. Three Ways To Prove Triangles Congruent SSS Postulate.

Triangle Congruence Proofs Foldable Practice Booklet Geometry Lessons Proof Writing Practices Worksheets

SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal.

How to do congruent triangle proofs. If three sides of one triangle are congruentto three sides of another triangle then the triangles are congruent. Provetwo triangles congruent by using the SSS SAS and the ASA Postulates. There are five ways to find if two triangles are congruent.

Two triangles are congruent if all pairs of corresponding sides are congruent and all pairs of corresponding angles are congruent. The following postulates and theorems are the most common methods for proving that triangles are congruent or equal. Corresponding Sides and Angles.

Tips for Working with Congruent Triangles in Proofs. Our first option cannot be correct because this figure does not give any information about the angles. If three sides of one triangle are equal to three sides of another triangle then the triangles are congruent.

But we have drawn over here is five different triangles and what I want to do in this video is figure out which of these triangles are congruent to which other of these triangles and to figure that out Im just over here going to write our our triangle congruence postulate so we know that two triangles are congruent if all of their sides are the same so side side side we also know they are. If there exists a correspondence between the vertices of two triangles such that the two sides and the. Given two triangles on a coordinate plane you can check whether they are congruent by using the distance formula to find the lengths of their sides.

Then write known information as statements and write Given for their reasons. SSS SAS ASA AAS and HL. If each side of one triangle is congruent to the corresponding side of another triangle then the triangles are congruent Figure 2.

If three sides of one triangle are congruent to three sides of a second triangle then the two triangles are congruent. A description of how to do a parallelogram congruent triangles proof. If there exists a correspondence between the vertices of two triangles such that three sides of one.

If three sides of one triangle are equal to three sides of. If two sides of a triangle are congruent then the angles opposite those sides are congruent. To write a congruent triangles geometry proof start by setting up 2 columns with Statements on the left and Reasons on the right.

The Angle-Side-Angle Theorem ASA states that if two angles and their included side are congruent to two angles and their included side to another triangle then these two triangles are congruent. By the SSS Postulate triangle ABC is congruentto triangle FGH. Two polygons are congruent if all the pairs of corresponding sides and all the pairs of corresponding angles are congruent.

For any of these proofs you have to have three consecutive anglessides ASA has a side that is between two angles or a leg of each angle and AAS has side that is a leg of only one of the angles. PowerPoint PPT presentation free to view. Two or more figures segments angles triangles etc that have the same shape and the same size.

Postulate 13 SSS Postulate. How do we prove triangles congruent. Fortunately we do not need to show all six of these congruent parts each time we want to show triangles congruent.

This could be proven using the SSS Theorem. This method is called side-side-side or SSS for short. If two angles and the included side of one triangle are.

Side Side SideSSS Angle Side Angle ASA. ASA SAS SSS Hypotenuse Leg Preparing for Proof. 123This video and the videos in my folders Intro to Geometry and Geometry are a s.

When all the sides of two triangles are congruent the angles of those triangles must also be congruent. SSS Side-Side-Side The simplest way to prove that triangles are congruent is to prove that all three sides of the triangle are congruent. Recall the SSS Congruence Theorem.

The symbol for corresponds to is. Converse of the Base Angles Theorem The converse of the base angles theorem states that if two angles of a triangle are congruent then sides opposite those angles are congruent. There are 5 combination methods that allow us to show triangles to be congruent.

Virtual Nerds patent-pending tutorial system provides in-context information hints and links to supporting tutorials synchronized with videos each 3 to 7 minutes long. These unique features make Virtual Nerd a viable alternative to private tutoring. AAA is not a proof of congruence but we can use AA as a proof of similarity for triangles.

Free Congruent Triangles Calculator - Find and prove triangle congruency step-by-step This website uses cookies to ensure you get the best experience.

Read more »

How To Prove If Triangles Are Congruent

B Name four pairs of corresponding angles. Learn how to prove that two triangles are congruent.

Congruent Triangles Math Side And Angle Rules For Congruent Triangles Triangle Math Math Infographic Basic Math Skills

Corresponding Sides and Angles.

How to prove if triangles are congruent. But the triangles are not congruent because the angle isnt between the two equal sides as per SAS congruence criteria. Given two triangles on a coordinate plane you can check whether they are congruent by using the distance formula to find the lengths of their sides. We discussed today the concepts about Proving Two Triangles are Congruent.

Side Side SideSSS Angle Side Angle ASA. Use HL for the congruent triangles in this example See Proof. 8 7 6 5 4 3 2 1 Name.

This is an extension of ASA. The sides you need are contained in ΔABD and ΔCBD. If three pairs of sides are congruent then the triangles are congruent by the above theorem.

If A B P Q B C Q R and A C P R then Δ A B C Δ P Q R. This theorem is also called the angle-angle-angle AAA theorem because if two angles of the triangle are congruent the third angle must also be congruent. There are many p.

Two or more triangles are said to be congruent if they have the same shape and size. Anyone of other two sides of both triangle are equal. I hope youll learn somethi.

Sometimes when you are trying to decide if triangles are congruent you need to identify other sides or angles that are congruent. The two sides of the triangles are equal. If any two right triangles have a congruent hypotenuse and a congruent corresponding leg the triangles are congruent.

Hypotenuse Leg Theorem is used to prove whether a given set of right triangles are congruent. Hypotenuse of both triangles are equal. Step 2 Therefore two sides and one angle of the triangles are equal.

In RHS congruence criteria Both triangle will have a right angle. _____ Unit 8 Day 3 - Proving Triangles Congruent Classwork 1. Its me again Mark ChavezWelcome to my latest vlog.

If two angles and any side of one triangle are congruent to two angles and any side of another triangle then the triangles are congruent. Free Congruent Triangles Calculator - Find and prove triangle congruency step-by-step This website uses cookies to ensure you get the best experience. Two triangles can be proved similar by the angle-angle theorem which states.

Define the angle-angle AA theorem. Use corresponding parts of congruent Δs are congruent. If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle the triangles are congruent.

A Name four pairs of vertical angles. In ASA since you know two sets of angles are congruent you automatically know the third sets are also congruent since there are 180º in each triangle. The triangles share side.

The Hypotenuse Leg HL Theorem states that If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle then the two right triangles are congruent. So it doesnt follow SAS congruence criteria. How do we prove triangles congruent.

If two triangles have two congruent angles then those triangles are similar. ASA SAS SSS Hypotenuse Leg Preparing for Proof. Also it is clear that the two vertically opposite angles are equal.

Read more »

How To Determine Congruent Triangles

The two sides of the triangles are equal. Side Angle Side SAS is a rule used to prove whether a given set of triangles are congruent.

Proving Triangles Congruent With Congruence Shortcuts Proving Triangles Congruent Geometry Lessons Teaching Geometry

Complete the explanation of your reasoning.

How to determine congruent triangles. Two or more triangles are said to be congruent if they have the same shape and size. Triangles are congruent when all corresponding sides interior angles are congruent. Solution for Determine whether the triangles are congruent.

2 triangles are congruent if they have. Given two triangles determine whether they are congruent and use that to find missing angle measures. Exactly the same three sides and.

The triangles will have the same size shape but 1 may be a mirror image of the other. Also it is clear that the two vertically opposite angles are equal. Learn how to solve for unknown variables in congruent triangles.

Learn how to solve for unknown variables in congruent triangles. Two or more triangles are said to be congruent if they have the same shape and size. Learn how to solve for unknown variables in congruent triangles.

Illustration of SAS rule. So it doesnt follow SAS congruence criteria. Remember that the included angle must be formed by the two sides for the triangles to be congruent.

In this case two triangles are congruent if two sides and one included angle in a given triangle are equal to the corresponding two sides and one included angle in another triangle. Given two triangles determine whether they are congruent and use that to find missing angle measures. If youre seeing this message it means were having trouble loading external resources on our website.

Two or more triangles are said to be congruent if they have the same shape and size. Use the triangle congruence criteria SSS SAS ASA and AAS to determine that two triangles are congruent. B Mark the congruent sides in the quadrilateral.

If they are congruent give the justification and give the triangle congruence statement. Use the triangle congruence criteria SSS SAS ASA and AAS to determine that two triangles are congruent. Determine if the triangles are congruent.

If youre seeing this message it means. Step 2 Therefore two sides and one angle of the triangles are equal. If the three sides of one triangle are congruent to the three sides of another triangle then the triangles are congruent Side-Side-Side or SSS.

For 4 and 5 mark the sides andor angles that you know are congruent from the given information. What else should you know is true without being told. To PR by the v to QR because PS.

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle then the triangles are congruent Side-Angle-Side or SAS. Determine congruent triangles practice Khan Academy. But the triangles are not congruent because the angle isnt between the two equal sides as per SAS congruence criteria.

Frac msquare msquare x2.

Read more »

What Is Congruent Triangles In Geometry

If the sides of two triangles are the same then the triangles must have the same angles and therefore must be congruent. HttpsbitlyTriangles_DMIn this video we will learn.

Congruent Triangles Worksheet Triangle Worksheet Congruent Triangles Worksheet Geometry Worksheets

Identify congruent figures and corresponding parts of congruent figures Prove that two triangles are congruent using various methods such as SSS SAS ASA AAS and HL Prove that parts of two triangles are congruent Identify and use properties of isosceles and equilateral triangles II.

What is congruent triangles in geometry. So if you have two triangles and you can transform for example by reflection one of them into the other while preserving the scale the two triangles are congruent. The congruence of two objects is often represented using the symbol. Basically triangles are congruent when they have the same shape and size.

The only difference is the length of their sides. A pair of congruent triangles is shown below. Congruent triangles are triangles that have the same size and shape.

Triangles that have exactly the same size and shape are called congruent triangles. The symbol for congruency is. 11 hours agoTriangle congruence when the longest sides the largest angles and one of the other sides are congruent.

The symbol for congruent is. We mark the corresponding equal sides with one line two lines and three lines as above. Congruency is a term used to describe two objects with the same shape and size.

We can represent this in a mathematical form using the congruent symbol. Congruent Triangles Two triangles that have the same three sides same length and the same angles same angle measures are said to be congruent or the same. In the above diagrams the corresponding sides are a and d.

In other words Congruent triangles have the same shape and dimensions. If two triangles have the same size and shape they are called congruent triangles. Two figures are congruent if they have the same shape and size.

If you flipreflect MNO over NO it is the same as ABC so these two triangles are congruent. If two triangles only share three congruent angles but not sides then the triangles are similar. Two triangles with equal corresponding angles may not be congruent to each other because one triangle might be an enlarged copy of the other.

This means that the corresponding sides are equal and the corresponding angles are equal. If we flip turn or rotate one of two congruent triangles they are still congruent. Two angles are congruent if their measures are exactly the same.

Two or more triangles are said to be congruent if their corresponding sides or angles are the side. The four triangles are congruent with each other regardless whether they are rotated or flipped. Also AB A B falls on P Q P Q BC B C falls on QR Q R and AC A C falls on P R P R.

This indicates that the corresponding parts of congruent triangles are equal. Thus these are congruent triangles. 000 Introduction017 what is the condit.

Choose 5 key terms from this unit that you. Congruent Triangles Definition In geometry triangles can be similar and they can be congruent. Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle.

Note that each side and angle of the triangle on the left has a corresponding congruent side or angle in the triangle on the right. Geometry A Unit 6 Congruent Triangles I. Similar triangles are proportional to each other and have the same interior angles.

Hence there is no AAA Criterion for Congruence. Congruent triangles Two or more triangles that have the same size and shape are called congruent triangles. The corresponding angles are x.

The triangles in Figure 1 are congruent triangles. To learn more about Triangles enrol in our full course now. This means A A falls on P P B B falls on Q Q and C C falls on R R.

2 Can an angle between the subdividing segments and the edges of a triangle be determined only by interior angles and the intersection of the segments. B and e.

Read more »

What Are The Properties Of Congruent Triangles

Triangles that have exactly the same size and shape are called congruent triangles. Two triangles are said to be congruent if one can be superimposed on the other such that each vertex and each side lie exactly on top of the other.

Prove Triangles Similar Via Aa Sss And Sas Similarity Theorems Notes Are More Fun When Doodling Mathematics Worksheets Doodle Notes Notes

А А 1.

What are the properties of congruent triangles. The diagonals are congruent and bisect each other divide each other equally. On the other hand triangles that are not congruent are called non-congruent triangles. Congruence is defined as agreement or harmony.

Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. Properties of a Rectangle Opposite sides are parallel and congruent. Basic properties of triangles The sum of the angles in a triangle is 180.

Congruent Triangles Section 4-4. If ΔАВС ΔА 1 В 1 С 1 then. In this blog we will understand how to use the properties of triangles to prove congruency between 22 or more separate triangles.

This is called the angle-sum property. This is the very first criterion of congruence. All angles are right.

The sum of the lengths of any two sides of. These triangles can be slides rotated flipped and turned to be looked identical. But you dont need to know all of them to show that two triangles are congruent.

These properties can be applied to segment angles triangles or any other shape. There are three very useful theorems that connect equality and congruence. Use the SSS Postulate to test for triangle congruence Use the SAS Postulate to test for triangle congruence.

Two angles are congruent if and only if they have equal measures. The first property of congruent triangles In congruent triangles their respective elements are congruent this follows from the definition of the congruence of triangles. SSS Criterion for Congruence SAS Criterion for Congruence ASA Criterion for Congruence AAS Criterion for Congruence RHS Criterion for Congruence.

If you flipreflect MNO over NO it is the same as ABC so these two triangles are congruent. Any triangle is defined by six measures three sides three angles. If there is a rigid transformation which maps to this means that In other words corresponding parts of congruent triangles are congruent.

The symbol for congruent is. The properties of congruent triangles are. If repositioned they coincide with each other.

The fundamental property of rigid motions of the plane is that they do not change angle measurements or side lengths. The symbol between the triangles indicates that the triangles are congruent. Two triangles are congruent if and only if all corresponding angles and sides are congruent.

Triangles to be congruent they should have two equal sides and one equal angle comprising the same sides. Two segments are congruent if and only if they have equal measures. The triangles in Figure 1 are congruent triangles.

Congruent triangles are triangles having all three sides of exactly the same length and all three angles of exactly the same measure. The meaning of the reflexive property of congruence is that a segment an angle a triangle or any other. The symbol of congruence is.

Reflexive property of congruence. So if you have two triangles and you can transform for example by reflection one of them into the other while preserving the scale the two triangles are congruent. SSSside side side SAS side angle side ASA angle side angle AAS angle angle side HL hypotenuse leg of a right triangle.

Proving Congruence SSS and SAS SOL. A triangle is said to be congruent to. G5 The student will b prove two triangles are congruent or similar given information in the form of a figure or statement using algebraic and coordinate as well as deductive proofs.

We know angle A. The three properties of congruence are the reflexive property of congruence the symmetric property of congruence and the transitive property of congruence. When two shapes sides or angles are congruent well use the symbol above.

The figure below will make things clear. Thus congruent triangles are mirror image of each other. SAS Congruence Rule SAS stands for Side-Angle-Side.

Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle. Basically triangles are congruent when they have the same shape and size.

Read more »

How To Prove Two Triangles In A Rectangle Are Congruent

Two or more triangles are said to be congruent if they have the same shape and size. Conclude that A C D is congruent to C A B.

Triangles Triangle Congruence Practice Sss Sas Asa Aas Hl 20 Task Teacher Tools Task Cards Task

We discussed today the concepts about Proving Two Triangles are Congruent.

How to prove two triangles in a rectangle are congruent. Two or more triangles are said to be congruent if they have the same shape and size. There are many p. Because they both have a right angle.

- Show that both pairs of opposite sides are parallel. Each diagonal of a parallelogram separates it into two congruent triangles. The second way to prove that the diagonals of a rectangle are congruent is to show that triangle ABD is congruent to triangle DCA Here is what is given.

- Show that both pairs of opposite sides are congruent. There are several different postulates you can use to prove that two triangles are congruent - that they are exactly the same size and shape. I hope youll learn somethi.

Segment AC segment BD. There are 5 different ways to prove that this shape is a parallelogram. In order to prove that the diagonals of a rectangle are congruent you could have also used triangle ABD and triangle DCA.

Call A the image of point A under the rotation and C the image of point C. A Name four pairs of vertical angles. Rectangle ABCD Here is what you need to prove.

- Show that one pair of sides is parallel and congruent. Two triangles can be proved similar by the angle-angle theorem which states. _____ Unit 8 Day 3 - Proving Triangles Congruent Classwork 1.

Click to see full answer. A 0 0 D a 0 B b 0 because AD AE so E acosθ asinθ. Draw the image of triangle A C D when it is rotated 180 about vertex D.

E is a point on the line AC so we can propose a coefficient λ that satisfies AC λ AE and 0 λ 1 then C λacosθ λasinθ. Show that A C D can be translated to C A B. Learn how to prove that two triangles are congruent.

The congruence postulates covered in this lesson are Side-Side-Side SSS Side-Angle-Side SAS Angle-Side-Angle ASA and Angle-Angle-Side AAS. Learn how to prove that two triangles are congruent. This theorem is also called the angle-angle-angle AAA theorem because if two angles of the triangle are congruent the third angle must also be congruent.

I AB AC Hypotenuse ii AD AD Common side Leg Hence the two triangles ABD and ACD are congruent by Hypotenuse-Leg HL theorem. Choose one of the methods. 8 7 6 5 4 3 2 1 Name.

Consecutive angles are supplementary A D 180. If one angle is right then all angles are right. If two triangles have two congruent angles then those triangles are similar.

Sometimes when you are trying to decide if triangles are congruent you need to identify other sides or angles that are congruent. Opposite angels are congruent D B. I Triangle ABD and triangle ACD are right triangles.

The diagonals of a parallelogram bisect each other. 3 months ago SAS stands for side angle side and means that we have two triangles where we know two sides and the included angle are equal. Explain why D A D A and why D C is parallel to A B.

B Name four pairs of corresponding angles. Its me again Mark ChavezWelcome to my latest vlog. If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle the triangles are congruent.

We do it by using the coordinate system like the picture. There are many p.

Read more »

Proving Triangles Congruent By Asa And Aas Calculator

Δ ABC Δ EDC by ASA Ex 5 B A C E D 26. Angle-Side-Angle ASA Congruence Postulate If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle then the triangles are congruent.

Congruent Triangle Rules Angle And Side Rules For Congruent Triangles If You Would Like More Math Infographics I Have A Math Infographic Math Math Methods

If two angles and the included side of a triangle are congruent to two angles and the included side of another triangle then the two triangles are congruent.

Proving triangles congruent by asa and aas calculator. Determine if whether each. Geometry Notes G6 ASA AAS Use Congruent Triangles Mrs. Grieser Page 2 Use Congruent Triangles to Prove Corresponding Parts Congruent CPCTC can be used to show corresponding parts of congruent triangles congruent Examples.

Proving Triangles are Congruent with ASA or AAS. Angle-side-angle ASA means well have a side in between two angles. Lets go over the angle-side-angle and angle-angle side.

A Explain how you would use the given information and congruent triangles to prove the statement. If it is not possible to prove that they are congruent write not possible. Δ ACB Δ ECD by SAS B A C E D Ex 6 27.

The ASA criterion for triangle congruence states that if two triangles have two pairs of congruent angles and the common side of the angles in one triangle is congruent to the corresponding side in the other triangle then the triangles are congruent. Isosceles and Equilateral Triangles 1Congruency in. Two methods we can use to prove that two triangles are congruent.

An included angle is an angle. Free Congruent Triangles Calculator - Find and prove triangle congruency step-by-step This website uses cookies to ensure you get the best experience. Proving Congruence ASA and AAS SOL.

CPCTC is an acronym for corresponding parts of congruent triangles are congruent. Triangle Congruence by ASA and AAS 1ASA and AAS Theorems N94 2Proving triangles congruent by ASA and AAS 23Z 34. Angle-Side-Angle ASA Congruence Postulate Two angles and the INCLUDED side.

2Proving triangles congruent by SSS and SAS VVZ 33. Using Corresponding Parts of Congruent Triangles 1Proofs involving corresponding parts of congruent triangles AKL 35. This theorem states that once two triangles are proven to be congruent then the three pairs of sides and angles that correspond must be congruent.

The Angle Angle Side postulate often abbreviated as AAS states that if two angles and the non-included side one triangle are congruent to two angles and the non-included side of another triangle then these two triangles are congruent. If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle then the triangles are congruent. Links Videos demonstrations for proving triangles congruent including ASA SSA ASA SSS and Hyp-Leg theorems.

If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle then the triangles are congruent. The SAS rule states that. The following video shows how to use CPCTC.

G5 The student will b prove two triangles are congruent or similar given information in the form of a figure or statement using algebraic and coordinate as well as deductive proofs. Definition and examples for the four triangle congruence postulates and theorems. A is congruent to H while C is congruent to Z.

We have MAC and CHZ with side m congruent to side c. Side-Angle-Side is a rule used to prove whether a given set of triangles are congruent. Congruent Triangles Section 4-5.

Determine if whether each pair of triangles is congruent by SSS SAS ASA or AAS. Use the ASA Postulate to test for triangle congruence Use the AAS Theorem to test for triangle congruence. By the ASA Postulate these two triangles are congruent.

Proving Triangles are Congruent ASA. If it is not possible to prove that they are congruent write not possible. Improve your math knowledge with free questions in Proving triangles congruent by ASA and AAS and thousands of other math skills.

Read more »

Difference Between Similar And Congruent In Geometry

While similiarity deals with only the shape of the figures you are dealing with also means that each and every side of one figure will bears a constant ratio with the respective sides of the second figure. The difference in size aspect means that a similar shape can never be congruent.

N Kupkntwc05dm

The concept of equality is a familiar concept in our day to day lives.

Difference between similar and congruent in geometry. As adjectives the difference between corresponding and congruent. Equal means that the magnitudes or sizes of any two in comparison are the same. Similar figures are the same shape but not necessarily the same size.

They have the same angle measures and the same side lengths. Congruent and equal are similar concepts in geometry but often misused and confused. Two objects are said to be congruent if one can be exactly.

In the figure below triangles and are congruent. You dont say that two shapes are equal or two numbers are congruent. Two 2-D shapes are congruent if they are identical in shape and size.

Angle Q is congruent to angle T and line QR is congruent to line TR Prove. Similarity means closely resembling each other but not quite the same. Is that corresponding is that have a similar relationship while congruent is corresponding in character.

The areas of two similar figures may be different. Congruence deals with objects while equality deals with numbers. It is important to recognize that the term congruent applies only to size and shape.

SimilarTwo figures are similar if they have the same shape but not necessarily the same size. However as a mathematical concept it has to be defined using stricter measures. Note that if two figures are congruent then they are also similar but not vice-versa.

Two things are said to be similar when they have a resemblance in appearance character or quantity. Difference Between Congruent and Similar Similar figures are the same in shape while congruent figures are the same in both shape and size. As adjectives the difference between proportional and congruent is that proportional is at a constant ratio to two magnitudes numbers are said to be proportional if the second varies in a direct relation arithmetically to the first while congruent is corresponding in character.

Great introduction the subject. Congruent triangles have both the same shape and the same size. Line PR is congruent to line SR Statement Proof 1.

Similar triangles have the same shape but not necessarily the same. Congruent figures are the same shape and size. Opposite sides are parallel D.

Opposite angles are congruent. Mathematically a shape can be similar in its basic shape a circle for example but different in size. Termdefinition CongruentCongruent figures are identical in size shape and measure.

The figures can be different colors or oriented in different ways and they will still be congruent as. All angles are congruent C. For example - 2 triangles are said to be similar to each other when they have same shape proportion and angles but.

The difference between congruent and similiar is that when you are proving something as congruent then both these figures are exactly coincide on each other if we will superpose it correspondingly. But it may or may not be identical. Mar 28 2014 - Game to reinforce the difference between similar and congruent shapes.

Supply the missing reasons to complete the proof. Im so confused 1. However the areas of two congruent figures are equal.

What is the difference between similarity and congruence. Difference between similar triangles and congruent triangles quadrilateral polygons geometry shapes K-12 mathematicsOur MantraInformation is Oppo.

Read more »

What Is The Difference Between Congruent And Corresponding

In simple if two angles are complement to a third angle the first two angles are equal in size. Congruent means identical while corresponding means having same designation.

Complementary And Supplementary Angles Types Of Angle Pairs Geometry Supplementary Angles Types Of Angles Complementary Angles

It is a specific scenario to solve a triangle when we are given 2 sides of a triangle and an angle in between them.

What is the difference between congruent and corresponding. The corresponding sides are AB AB BC BC CD CD. It is the equivalent concept of equality used in geometry. In geometry the words denote having the same size and shape as in a description of identical parallel lines or of corresponding lines in two geometrical figures that are mirror images of each other.

The noun congruence and its. With reference to polygons the terms corresponding and congruent are different animals. As adjectives the difference between congruent and incongruent is that congruent is corresponding in character while incongruent is out of place incompatible inharmonious not congruent.

As adjectives the difference between corresponding and congruent is that corresponding is that have a similar relationship while congruent is corresponding in character. If two corresponding angles and one corresponding sides of a triangle are equal then they are congruent under ASA congruence criteria. As a noun corresponding is action of the verb to correspond.

The noun congruence and its adjectival form congruent refer to agreement or coincidence. Is that congruent is corresponding in character while concurrent is happening at the same time. Congruent normally refers to angles and trianglescongruent angles are to each other and have a common reference point.

The distinction is slight as the meanings are nearly identical. In the context of geometry congruent means equal in both figures shape and sizes. Same in cases 1 and 2 if they are not corresponding they will not be congruent.

If triangle ABC is congruent to triangle DEF the relationship can be written mathematically as. Whats the difference between congruent and congruous. In fact there are far more similar shapes than the congruent unique one.

As a verb corresponding is. If you try to use angle-side-side that will make an ASS out of you. Congruence also has other applications in higher mathematics.

As adjectives the difference between congruent and concurrent. Congruent angles are angles that have the same measure. Complements of congruent angles are congruent.

Shapes which are similar CAN also be congruent but shapes which are congruent are ALWAYS similar. Corresponding angles are formed when two lines are cut by a transversal. See ambiguous case of sine rule for more information ASA.

In similarity corresponding angles are equal but sides may or may not be. An example is given below. As adjectives the difference between congruent and equal is that congruent is corresponding in character while equal is label the same in all respects.

Is that congruent is corresponding in character while concurrent is happening at the same time. In mathematicslangen terms the difference between congruent and equal is that congruent is mathematics coinciding exactly when superimposed while equal is mathematics to be equal to to have the same value as. Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in measure.

Or in simpler words if one can be considered as an exact copy of the other then the objects are congruent irrespective of the positioning. However the former term is usually employed quantitatively while the latter word is generally used qualitatively. These triangles need not be congruent or similar.

Extending the sides proportionally produces similar shapes. If you take two polygons ABCDand ABC. Consider two angles that are equal in size.

Is that proportional is at a constant ratio to two magnitudes numbers are said to be proportional if the second varies in a direct relation arithmetically to the first while congruent is corresponding in character. As adjectives the difference between congruent and concurrent. This is true for all other cases.

Difference between congruence and Similarity The Basic Difference between congruence and Similarity is that geometric figures are congruent if they have the same shape and dimension regardless of their orientation or position in turn they have similarities if they have the same shape regardless of the size they present. Corresponding angles have the same position with respect to the line. Congruent triangles have be proven that corresponding angles are and.

The complementary angles of these angles are equal to each other. When the two lines intersected by the transversal are parallel corresponding angles are congruent alternate interior angles are congruent alternate exterior angles are.

Read more »

How To Find X In Congruent Triangles

Illustration of SAS rule. Virtual Nerds patent-pending tutorial system provides in-context information hints and links to supporting tutorials synchronized with videos each 3 to 7 minutes long.

3 2 Three Ways To Prove Triangles Congruent Lesson Proving Triangles Congruent Math Methods Teaching Geometry

These unique features make Virtual Nerd a viable alternative to private tutoring.

How to find x in congruent triangles. Find the value of x in the triangle. Find the side lengths using the Distance Formula. Semicircle then the right triangle with 5 ft on the top.

Learn how to solve for unknown variables in congruent triangles. In this case two triangles are congruent if two sides and one included angle in a given triangle are equal to the corresponding two sides and one included angle in another triangle. Find angles in congruent triangles Our mission is to provide a free world-class education to anyone anywhere.

But we have drawn over here is five different triangles and what I want to do in this video is figure out which of these triangles are congruent to which other of these triangles and to figure that out Im just over here going to write our our triangle congruence postulate so we know that two triangles are congruent if all of their sides are the same so side side side we also know they are. Show all your work. The sum of angles in a triangle are 180 and if you have an iscoseles triangle the angles opposite the congruent sides are congruent also.

Please support my channel by becoming a Patron. Corresponding parts of Congruent triangles CPCTC are congruent. Free Congruent Triangles Calculator - Find and prove triangle congruency step-by-step This website uses cookies to ensure you get the best experience.

Learn how to solve for unknown variables in congruent triangles. Use 314 for π and round to the nearest tenth. The Hypotenuse-Leg HL Rule states that.

Khan Academy is a 501c3 nonprofit organization. Two or more triangles are said to be congruent if they have the same shape and size. In the right triangles ΔABC and.

In this non-linear system users are free to take whatever path through the material best serves their needs. Given two triangles determine whether they are congruent and use that to find missing angle measures. Learn how to solve for unknown variables in congruent triangles.

Side Angle Side SAS is a rule used to prove whether a given set of triangles are congruent. A figure is composed of a semicircle and a right triangle. So if you have x as one of the angles opposite and a vertex angle of x 30 the other opposite angle is also x so x x x 30 180 which you can solve.

Distance x 2 x 1 2 y 2 y 1 2. Remember that the included angle must be formed by the two sides for the triangles to be congruent. Show all of your work.

Two or more triangles are said to be congruent if they have the same shape and size. If youre seeing this message it means were having trouble loading external resources on. Hence proved that a line segment connecting two midpoints of the opposite sides of a triangle is parallel to the third side and is half the third side then that line segment is the midsegment of the triangle.

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle then the two right triangles are congruent. Determine the area of the shaded region. Two or more triangles are said to be congruent if they have the same shape and size.

Read more »

Congruent Triangles Sss Sas Asa Aas Hl Worksheet Answers

SSS stands for side side side and means that we have two triangles with all three sides equal. Geometry worksheet congruent triangles asa and aas answers from triangle congruence worksheet 1 answer key source.

Pin On Geom Congruent Triangles

Asa aas and hl practice a 1.

Congruent triangles sss sas asa aas hl worksheet answers. 1 1 A 2 D 3 C 4 A. This activity includes three parts that can be done all in one lesson or spread out across a unit on congruent triangles. Links Videos demonstrations for proving triangles congruent including ASA SSA ASA SSS and Hyp-Leg theorems.

1 HL 2 SSS 3 AAS 4 Not congruent 5 ASA 6 SSS 7 SAS 8 SAS 9 AAS-1-. Triangle Congruence Oh My Worksheet - Math Teacher Mambo November 2010. The quiz will assess your understanding of concepts.

The SSS rule states that. These congruent triangles notes and worksheets covercongruent triangle introcongruent shortcuts sss sas asa aas hlcongruent triangle measures with algebraproofs with and without cpctceach topic includes at least one practice worksheet. You will need a separate piece of paper to show all your work.

SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal. There are five ways to find if two triangles are congruent. A X B C Y Z.

SSS SAS ASA AAS and HL. Answers to Assignment ID. Improve your math knowledge with free questions in Proving triangles congruent by SSS SAS ASA and AAS and thousands of other math skills.

Side-Side-Side is a rule used to prove whether a given set of triangles are congruent. State if the two triangles are congruent. Sss and sas of another triangle then the triangles are congruent.

The origin of the word congruent is from the Latin word congruere meaning correspond with or in harmony. Asa and aas theorems. Triangle Congruence a Determine whether the following triangles are congruent b If they are name the triangle congruence pay attention to proper correspondence when naming the triangles and then identify the Theorem or Postulate SSS SAS ASA AAS HL that supports your conclusion.

Share skill IXL - SSS SAS ASA and AAS Theorems Geometry practice There are five ways to find if two triangles are congruent. Name the postulate if possible that makes the triangles congruent. If three sides of one triangle are equal to three sides of another triangle then the triangles are congruent.

Congruent Triangles Sss And Sas Worksheet Answers Nidecmege. I can prove triangles are congruent using SSS ASA. Hl Triangle Congruence Worksheet Answers.

Sas Sss Asa Aas And Hl. State what additional information is required in order to know that the triangles are congruent for the reason given. Hypotenuse- Leg HL Congruence Theorem.

If they are state how you know. Congruent Triangles by SSS SAS ASA AAS and HL - practice review activity set for triangle congruence with shortcuts. If you slid triangle a to the right it would exactly answer.

SSS ASASAS AAS and HL State if the two triangles are congruent. A collection of congruent triangles worksheets on key concepts like congruent parts of congruent triangles congruence statement identifying the postulates congruence in right triangles and a lot more is featured here for the exclusive use of 8th grade and high school students. Triangle congruence online worksheet for 9.

11 ASA S U T D 12 SAS W X V K 13 SAS B A C K J L 14 ASA D E F J K L 15 SAS H I J R S T 16 ASA M L K S T U 17 SSS R S Q D 18 SAS W U V M K-2-. A sample problem is students will prove the congruence of each pair of triangles. Play this game to review Geometry.

If they are state how you know. SSS SAS ASA AAS and HL. In the diagrams below if AB RP BC PQ and CA QR then triangle ABC is congruent to triangle RPQ.

Geometry K5 SSS SAS ASA and AAS Theorems LER. The diagonal is the hypotenuse of an isosceles right triangle. Worksheet template 4 6 using congruent triangles cpctc from triangle congruence worksheet answers source.

You can print the two sets of Triangle Cards for worksheets A and C on colored cardstock if desired. 234 3-11 19 22-25 31 15 problems Triangle Congruence Worksheet 1 Friday 11912. 1 A SSS B SAS C AAS D Not congruent 2 A AAS B SAS.

ASA AAS and HL I can prove triangles are congruent using ASA AAS and HL I can mark pieces of a triangle congruent given how they are to be proved. If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and leg of a second right triangle then the two triangles are congruent. If three sides of one triangle are equal to three sides of another triangle the triangles are congruent.

SSS side side side. 21 A SSS B ASA C AAS D SAS 22 A AAS B SAS C ASA D Not congruent.

Read more »