Properties Of Right Angle Triangle In Hindi

The formula for Area of Triangle. Area of any triangle ½ base height.

Ncert Solutions For Class 9 Maths Chapter 6 Lines And Angles 2019 20 Math Chapter Solutions

For Example In ABC BAC is 90 right angle and ACB and ABC are less than 90 acute angle.

Properties of right angle triangle in hindi. When we study the properties of a triangle we generally take into consideration the isosceles triangles as this triangle is the mixture of equality and inequalities. Isosceles Right Angel Triangle Median as Perpendicular in Hindi 10m 53s. The side that is.

Prove geometric mean property of right angled triangle. One angle of the triangle always measures 90degree. A triangle which has all its three angles are of equal measurement ie.

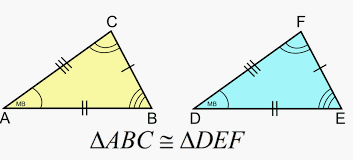
Let there be a right angle ABC and circle M with AC as a diameter. This is a scalene right-angled triangle since all three angles are different. A triangle whose one angle is a right angle that is 90 is called a right angled triangle or right triangle.

In figure ABC is a right triangle right angled at A. Then we know A C because the circle centered at the origin has AC as diameter and A B B C 0 because ABC is a right angle. Properties of Right - Angled Triangle All the properties of right-angled triangle are mentioned below.

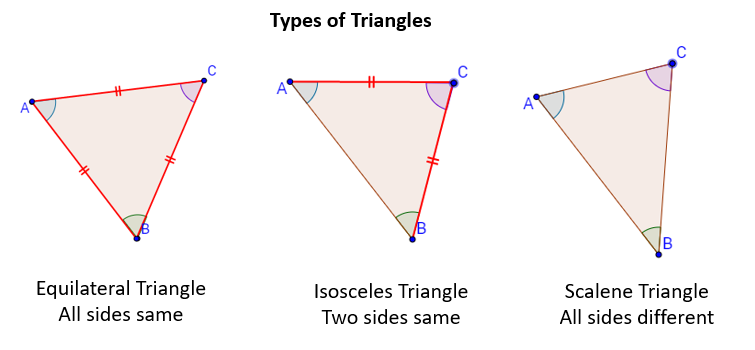
Isosceles triangles and scalene triangles come under this category of triangles. D lies on BA produced and DE BC intersecting AC at F. The angles of this triangle are in the ratio 1.

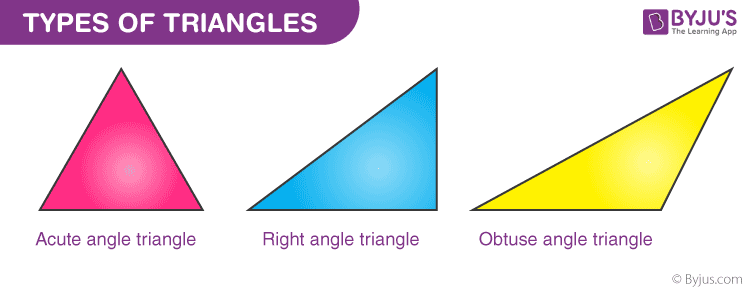
When one angle of a triangle is exactly 90 then the triangle is known as the Right Angle Triangle. To recall an acute angle is an angle that is less than. A triangle with one angle equal to 90 is called right-angled triangle.

Angles opposite to equal sides of an isosceles triangle are equal to each other. The hypotenuse is the longest side of the right-angle triangle. Isosceles Right Angel Triangle Introduction in Hindi 11m 23s.

The construction of the right angle triangle is also very easy. Triangles part 2 Hindi Isosceles triangle sides and angles relation Hindi This is the currently selected item. The sides opposite to these angles will be in the ratio 1.

This is a right-angled triangle since one angle 90 0. In the figure above the side opposite to the right angle BC is called the hypotenuse. Depending upon the sides and angles of a triangle we have different types of triangles which we will discuss hereTriangle is an important concept which taught in most of the classes like Class 7 Class 8 Class 9 Class 10 and in Class 11.

A Right-angled Triangle must have one angle exactly equal to 90 it may be scalene or isosceles but since one angle has to be 90 hence it can never be an equilateral triangle. For a Right triangle ABC BC 2 AB 2 AC 2. In the figure above the side opposite to the right angle BC is called the hypotenuse.

Right Angled Triangle RAT When one angle of a triangle is 90 and the other two angles are acute less than 90 then we call such a triangle as a RAT. 60 is called an equiangular triangle. This is called the Pythagorean Theorem.

Right angle Triangle. The sides of an equiangular triangle are all the same length congruent and. For a Right triangle ABC BC 2 AB 2 AC 2.

If one of the angles is 90 and the other two angles are equal to 45 each then the triangle is called an Isosceles Right Angled Triangle where the adjacent sides to 90 are equal in length. An acute angle triangle or acute-angled triangle is a triangle in which all the interior angles are acute angles. This is called the Pythagorean Theorem.

A triangle whose one angle is a right-angle is a Right-angled triangle or Right triangle. Isosceles Right Angel Triangle Median and Perpendicular in Hindi 12m 13s. It follows 0 A B B C A B B A A 2 B 2.

Only a triangle that satisfies this condition is a right triangle. A triangle whose one angle is a right-angle is a Right-angled triangle or Right triangle. In the triangle above 5 2 4 2 3 2.

Let Ms center lie on the origin for easier calculation. A triangle is a polygon that consists of three sides three edges three vertices and the sum of internal angles of a triangle equal to 180. Find angles in isosceles triangles.

In the triangle above 5 2 4 2 3 2. Scalene Triangle Introduction and basic question in Hindi 11m 47s. Only a triangle.

Properties of Right-angled Triangle. Angles opposite to equal sides of an isosceles triangle are equal to each other. Above were the general properties of the Right angle triangle.

Read more »

How To Do Congruent Triangle Proofs

In this non-linear system users are free to take whatever path through the material best serves their needs. Three Ways To Prove Triangles Congruent SSS Postulate.

Triangle Congruence Proofs Foldable Practice Booklet Geometry Lessons Proof Writing Practices Worksheets

SSS side side side SSS stands for side side side and means that we have two triangles with all three sides equal.

How to do congruent triangle proofs. If three sides of one triangle are congruentto three sides of another triangle then the triangles are congruent. Provetwo triangles congruent by using the SSS SAS and the ASA Postulates. There are five ways to find if two triangles are congruent.

Two triangles are congruent if all pairs of corresponding sides are congruent and all pairs of corresponding angles are congruent. The following postulates and theorems are the most common methods for proving that triangles are congruent or equal. Corresponding Sides and Angles.

Tips for Working with Congruent Triangles in Proofs. Our first option cannot be correct because this figure does not give any information about the angles. If three sides of one triangle are equal to three sides of another triangle then the triangles are congruent.

But we have drawn over here is five different triangles and what I want to do in this video is figure out which of these triangles are congruent to which other of these triangles and to figure that out Im just over here going to write our our triangle congruence postulate so we know that two triangles are congruent if all of their sides are the same so side side side we also know they are. If there exists a correspondence between the vertices of two triangles such that the two sides and the. Given two triangles on a coordinate plane you can check whether they are congruent by using the distance formula to find the lengths of their sides.

Then write known information as statements and write Given for their reasons. SSS SAS ASA AAS and HL. If each side of one triangle is congruent to the corresponding side of another triangle then the triangles are congruent Figure 2.

If three sides of one triangle are congruent to three sides of a second triangle then the two triangles are congruent. A description of how to do a parallelogram congruent triangles proof. If there exists a correspondence between the vertices of two triangles such that three sides of one.

If three sides of one triangle are equal to three sides of. If two sides of a triangle are congruent then the angles opposite those sides are congruent. To write a congruent triangles geometry proof start by setting up 2 columns with Statements on the left and Reasons on the right.

The Angle-Side-Angle Theorem ASA states that if two angles and their included side are congruent to two angles and their included side to another triangle then these two triangles are congruent. By the SSS Postulate triangle ABC is congruentto triangle FGH. Two polygons are congruent if all the pairs of corresponding sides and all the pairs of corresponding angles are congruent.

For any of these proofs you have to have three consecutive anglessides ASA has a side that is between two angles or a leg of each angle and AAS has side that is a leg of only one of the angles. PowerPoint PPT presentation free to view. Two or more figures segments angles triangles etc that have the same shape and the same size.

Postulate 13 SSS Postulate. How do we prove triangles congruent. Fortunately we do not need to show all six of these congruent parts each time we want to show triangles congruent.

This could be proven using the SSS Theorem. This method is called side-side-side or SSS for short. If two angles and the included side of one triangle are.

Side Side SideSSS Angle Side Angle ASA. ASA SAS SSS Hypotenuse Leg Preparing for Proof. 123This video and the videos in my folders Intro to Geometry and Geometry are a s.

When all the sides of two triangles are congruent the angles of those triangles must also be congruent. SSS Side-Side-Side The simplest way to prove that triangles are congruent is to prove that all three sides of the triangle are congruent. Recall the SSS Congruence Theorem.

The symbol for corresponds to is. Converse of the Base Angles Theorem The converse of the base angles theorem states that if two angles of a triangle are congruent then sides opposite those angles are congruent. There are 5 combination methods that allow us to show triangles to be congruent.

Virtual Nerds patent-pending tutorial system provides in-context information hints and links to supporting tutorials synchronized with videos each 3 to 7 minutes long. These unique features make Virtual Nerd a viable alternative to private tutoring. AAA is not a proof of congruence but we can use AA as a proof of similarity for triangles.

Free Congruent Triangles Calculator - Find and prove triangle congruency step-by-step This website uses cookies to ensure you get the best experience.

Read more »

What Does An Angle Bisector Do In A Triangle

Triangle Angle Bisector Theorem States that an angle bisector of a. Every triangle has three angle bisectors.

Dynamic Geometry Problem 887 Triangle Altitude Angle Bisector Perpendicular Midpoint Concyclic Mathematics Education Geometry Problems Teaching Geometry

Here I is the incenter of Δ P Q R.

What does an angle bisector do in a triangle. An angle bisector is a line segment ray or line that divides an angle into two congruent adjacent angles. In a right angled triangle the legs adjacent to the right angle are equal to a and b. An angle bisector divides an angle.

Triangle Angle Bisector Theorem file name. As you can see in the picture below the angle bisector theorem states that the angle bisector like segment AD in the picture below divides the sides of the a triangle proportionally. So AOC BOC which means AOC and BOC are congruent angles.

The three angle bisectors are concurrent. HttpsbitlyTriangles_DMIn this video we will learn. In a triangle an angle bisector is a line which bisects an angle of the triangle.

Prove that the length of the bisector of the right angle is equal to a b 2 a b. The bisector line segment is perpendicular to the bottom line of the triangle the bisector line segment is equal in length to itself and the angle thats being bisected is divided into two angles with equal measures. The bisector is the thing doing the cutting.

The three angle bisectors of the angles of a triangle meet in a single point called the incenter. An angle bisector in a triangle is a segment drawn from a vertex that bisects cuts in half that vertex angle. Im a bit confused.

In Figure is an angle bisector in Δ ABC. A line that splits an angle into two equal angles. To learn more about Triangles enrol in our full course now.

Every triangle has three angle bisectors. While approaching this question I was very puzzled as to how I would end up with this expression. In an angle bisector it is a line passing through the vertexof the angle that cuts it into two equal smaller angles.

Line segment OC bisects angle AOB above. When you bisect the angle of a triangle it divides the opposite side into two line segments. An angle bisector divides an angle into two equal parts.

Triangle Angle Bisector Theorem. Extend C A to meet B E at point E. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.

Every triangle has three angle bisectors. That is for any triangle ABC the bisector of the angle at C divides the opposite side into segments of length x and y such that. Bisect means to divide into two equal parts Try moving the points below the red line is the Angle Bisector.

The bisector of an angle of a triangle divides the opposite side into segments that are proportional to the adjacent sides. The point of concurrency of the angle bisectors is called the incenter of the triangle and it always lies inside the triangle. The picture below shows the proportion in action.

The angle bisector of an angle of a triangle is a straight line that divides the angle into two congruent angles. How Many Angle Bisectors does a Triangle Have In ΔABC B a B b and B c are the3 angle bisectors. According to the definition of perpendicular bisector it is a line that divides a line segment into two equal parts and is also perpendicular to it.

By the Angle Bisector Theorem B D D C A B A C. The incenter is equidistant from the sides of the triangle. By the Side-Splitter Theorem.

The angle bisector theorem states that the relative size of these two line segments is proportional to the relative size of the other two sides of the triangle. The following figure illustrates this. This video shows how to construct the angle bisectors of a triangle using a compass and straightedgeComplete Video List.

The Angle-Bisector theorem states that if a ray bisects an angle of a triangle then it divides the opposite side into segments that are proportional to the other two sides. The Angle-Bisector theorem involves a proportion like with similar triangles. In the figure above JK is the bisector.

Draw B E A D. 000 Introduction014 what is an angle b.

Read more »

Triangle Congruence Sss Sas Asa Aas Hl Oh My Worksheet

The three sides of one are exactly equal as the three sides of the other. Links Videos demonstrations for proving triangles congruent including ASA SSA ASA SSS and Hyp-Leg theorems.

Triangle Congruence Sss Sas Asa Aas Hl Oh My Quiz Quizizz

Name the postulate if possible that makes the triangles congruent.

Triangle congruence sss sas asa aas hl oh my worksheet. Triangle congruence sss sas asa aas hl oh my worksheet answer key Congruent triangles are triangles with the same sides and angles. 1 L I2e0 p1X37 bK DugtBac MSOoXfdtSw7a3r Me8 iL HLXCJm C zA mlhli Brai Eg ahatNsL Zr OeIsweqrOv0e dwY Congruence Postulates. The three corners of one of them have the same angle as the other.

Triangle Congruence Sss Sas Asa Aas Hl - Displaying top 8 worksheets found for this concept. SSS SAS ASA AAS and HL Hypotenuse and Leg TheoremVery useful for a review or great for interactive notebooksCheck the. It contains 5 theorems.

E Worksheet by Kuta Software LLC ESl Geometry Mr. T3 T4 SSS and SAS congruence ASA AAS Congruence Right Triangle Hypotenuse and legs Isosceles and Equilateral Triangles Checks for Understanding Intentional strategies used throughout the lesson to gage your students level of understanding. Triangle Congruence Worksheet 2.

Join us as we explore the five triangle congruence theorems SSS postulate SAS postulate ASA postulate AAS postulate and HL postulate. Triangle congruence sss sas asa aas hl oh my worksheet answer key Congruent triangles are triangles with the same sides and angles. A minimum of 3 strategies should be used each lesson.

Gina Wilson 2014 Unit 4 Congruent Triangles - Displaying top 8 worksheets found for this concept. I can prove triangles are congruent using SSS ASA. Congruent Triangles Theorems Foldable SSSSASASAAASHLThis foldable summarizes the theorems to prove when triangles are congruent.

Take your time this is a grade. Triangle Congruence Postulates Five ways are available for finding two congruent triangles. E U mMSaZdfe B 3waiOtxhD XILn1f NirnMiztAe8 XGze UoLmSeXt Xrbyu.

Triangle Congruence a Determine whether the following triangles are congruent b If they are name the triangle congruence pay attention to proper correspondence when naming the triangles and then identify the Theorem or Postulate SSS SAS ASA AAS HL that supports your conclusion. ASA AAS and HL I can prove triangles are congruent using ASA AAS and HL I can mark pieces of a triangle congruent given how they are to be proved. Some of the worksheets for this concept are 4 s sas asa and aas congruence Unit 4 triangles part 1 geometry smart packet Triangle congruence s sas asa aas hl oh my work 4 asa and aas congruence Triangle proofs s sas asa aas Triangle congruence work geometry 4 s and sas congruence Triangle.

There are five ways to find if two triangles are congruent. SSS ASASAS AAS and HL State if the two triangles are congruent. This geometry video tutorial provides a basic introduction into triangle congruence theorems.

11 ASA S U T D 12 SAS W X V K 13 SAS B A C K J L 14 ASA D E F J K L 15 SAS H I J R S T 16 ASA M L K S T U 17 SSS R S Q D 18 SAS W U V M K-2-. SSS SAS ASA AAS and HL. 1 day agoJul 30 2019 Geometry Practice.

SSS or the side side. Triangle Congruence Oh My Worksheet - Congruent Triangles Worksheet Problems Solutions Triangle Worksheet Congruent Triangles Worksheet Triangles Activities. 6 Jun 2015 Geometry.

SSS side side side SSS stands for side side side and means that we have two triangles with all. State what additional information is required in order to know that the triangles are congruent for the reason given. 234 3-11 19 22-25 31 15 problems Triangle Congruence Worksheet 1 Friday 11912.

By the end of thi. Some of the worksheets for this concept are Unit 1 angle relationship answer key gina wilson Proving triangles congruent Gina wilson all things algebra 2014 answers pdf Unit 2 syllabus parallel and perpendicular lines 4 s sas asa and aas congruence 4 congruence and triangles Unit 1 angle. A collection of congruent triangles worksheets on key concepts like congruent parts of congruent triangles congruence statement identifying the postulates congruence in right triangles and a lot more is featured here for the exclusive use of 8th grade and high school students.

Play this game to review Geometry. Play this game to review Geometry. Every time you click the new worksheet button you will get a brand new printable pdf worksheet on congruence of triangles.

4 f2x0x1M1W xKLuWtZat uSQolfut9w0azroeM 8LTLICX. The origin of the word congruent is from the Latin word congruere meaning correspond with or in harmony. It explains how to prove if two triangles are congruent using.

Compare the triangles and determine whether they can be proven congruent if possible by SSS SAS ASA AAS HL or NA not congruent or not enough information.

Read more »

What Does Congruent Triangle Mean

Note that each side and angle of the triangle on the left has a corresponding congruent side or angle in the triangle on the right. Learn about congruent triangles theorems.

Congruent Triangles Read Geometry Ck 12 Foundation

An included side is the side between the two given angles.

What does congruent triangle mean. One way to classify a triangle is by its sides. If two triangles are congruent then each part of the triangle side or angle is congruent to the corresponding part in the other triangle. Two shapes that are the same size and the same shape are congruent.

There are five ways to test that two triangles are congruent. Triangles that have exactly the same size and shape are called congruent triangles. Congruent angles have the exact same measure.

Two triangles are said to be congruent if all 33 of their angles and all 33 of their sides are equal. How to pronounce definition audio dictionary. They are identical in size and shape.

If in two right triangles the hypotenuse and one leg are equal then the triangles are congruent. These two triangles are of the same size and shape. For any set of congruent geometric figures corresponding sides angles faces etc.

To remember this important idea some find it helpful to use the acronym. Previous section Congruence Next section Problems. The triangles in Figure 1 are congruent triangles.

You can find the angles or sides of one of them from the other. Of a substance or compound not undergoing a change in composition when undergoing a reaction as with congruent melting. By proving the congruence of triangles we can show that polygons are congruent and eventually make conclusions about the real world.

A pair of congruent triangles is shown below. For a list see Congruent Triangles. Two or more triangles or polygons are said to be congruent if they have the same shape and size.

Of figures coinciding at all points when superimposed. Shapes A B E and G are congruent. This way of classifying a triangle is based on the number of congruent sides a triangle has.

The symbol for congruent is. Of or relating to two numbers related by a congruence. Congruent Triangles - Hypotenuse and leg of a right triangle.

It means if the corresponding hypotenuse and one side of two or more triangles are equal and they are both right angled triangle then they are congruent to each other. Although these are 66 parameters we only need 33 to prove congruency. Thus we can say that they are congruent.

When a triangle is said to be congruent to another triangle it means that the corresponding parts of each triangle are congruent. Congruent sides or segments have the exact same length. Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle.

Thus these are congruent triangles. If two triangles only share three congruent angles but not sides then the triangles are. The Angle-Side-Angle ASA Rule states that.

If two angles and the included side of one triangle are equal to two angles and included side of another triangle then the triangles are congruent. For example the above picture the shown two triangles are congruent to each other. Having a difference divisible by a modulus.

Congruency between sides of a triangle is. This is one of them HL. Video shows what congruent means.

Two right triangles are congruent if the hypotenuse and one corresponding leg are equal in both triangles. Hypotenuse is the longest side of any right angled triangle. Exactly equal in size and shape.

Read more »

How To Find Congruent Triangle Proofs

A triangle with three congruent sides is a special type of isosceles triangle and is more specifically called equilateral. Use this immensely important concept to prove various geometric theorems about triangles and parallelograms.

Math Teacher Mambo Proving Triangles Congruent Proving Triangles Congruent Math Teacher Teaching Geometry

We can use this knowledge of congruent sides and angles to find the.

How to find congruent triangle proofs. Go to your personalized Recommendations wall to find a skill that looks interesting or select a skill plan that aligns to your textbook state standards or standardized test. We would like to show you a description here but the site wont allow us. If C is the midpoint of AE then AC must be congruent to CE because of the definition of a midpoint.

Congruent Triangles Build similar triangles by combining sides and angles. In the above diagrams the blue triangles are all congruent and the yellow squares are congruent. First we need to find the area of the big square two different ways.

This is an extension of ASA. The two wheels are both circles and the distance around them is the same. In many cases it is sufficient to establish the equality of three corresponding parts and use one of the following results to deduce the congruence of the two triangles.

CPCTC is commonly used at or near the end of a proof which asks the student to show that two angles or two sides are congruent. If triangle ABC is congruent to triangle DEF the relationship can be written mathematically as. Because angles of a triangle always add to make 180.

AA SAS and SSS. In Exercise 3-8 explain how to prove that the statement is. It means that once two triangles are proven to be congruent then the three pairs of sides that correspond must be congruent and the three pairs of angles that correspond must be congruent.

Geoboard Use geoboards to illustrate area perimeter and rational number concepts. Insert congruent right triangles left-facing COW and right facing PIG. 405 22 2009-02-08.

675 36 2009-02-08. Learn what it means for two figures to be congruent and how to determine whether two figures are congruent or not. If the given information contains definitions be.

Here are right triangles COW and PIG with hypotenuses of sides w and i congruent. 548 29 2009-02-08. In ASA since you know two sets of angles are congruent you automatically know the third sets are also congruent since there are 180º in each triangle.

These transformations lead to the criterion for triangle similarity that two pairs of corresponding angles are congruent. The definitions of sine cosine and tangent for acute angles are founded on right triangles and similarity and with the Pythagorean Theorem are fundamental in many real-world and theoretical situations. _____ parts of congruent triangle are congruent.

Not sure where to start. Let us write that the area of the large square is the area of the small square plus the total area of all 4 congruent right triangles in the corners of the large square. Proof 1 In the figure below are shown two squares whose sides are a b and c.

First lets find the area using the area formula for a square. Use this immensely important concept to prove various geometric theorems about triangles and parallelograms. If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle the triangles are congruent.

When working with congruent triangles remember to. Learn what it means for two figures to be congruent and how to determine whether two figures are congruent or not. This allows you prove that at least one of the sides of both of the triangles are congruent.

Tips for Preparing Congruent Triangle Proofs. Geoboard - Isometric Use geoboard to illustrate three-dimensional shapes. There are three ways to find if two triangles are similar.

Similar Similar Triangles Similar Triangle Theorems Congruent Congruent Triangles Finding Congruent Triangles Trigonometry Index. The other two sides are legs. IXL offers hundreds of Geometry skills to explore and learn.

Start by marking the given information on your diagram using hash marks arcs etc. The hypotenuse of a right triangle is the longest side. Hyperbolic Geometry used in Einsteins General Theory of Relativity and Curved Hyperspace.

Come up with some of your own real-world examples of congruent figures and explain why they are congruent. IXL offers hundreds of Geometry. Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in measure.

C is the midpoint of AE BE is congruent to DA. Now lets find the area by finding the area of each of the components and then sum the areas. NonEuclid is Java Software for Interactively Creating Straightedge and Collapsible Compass constructions in both the Poincare Disk Model of Hyperbolic Geometry for use in High School and Undergraduate Education.

Proofs Of Pythagorean Theorem. Either leg can be congruent between the two triangles. Legs o and g are also congruent.

Using the following givens prove that triangle ABC and CDE are congruent. Monitoring Progress and Modeling With Mathematics. WRITING Describe a situation in which you might choose to use indirect measurement with congruent triangles to find a measure rather than measuring directly.

Read more »

What Are Angle Bisectors Of A Triangle

The three angle bisectors are concurrent. Therefore according to the criterion for the congruence of right triangles by an angle and the hypotenuse the triangles under consideration are congruent.

Pin On Geometry Theorems And Problems Math

Here I is the incenter of Δ P Q R.

What are angle bisectors of a triangle. Angle Bisectors of Triangles Date_____ Period____ Each figure shows a triangle with one of its angle bisectors. The three angle bisectors of the angles of a triangle meet in a single point called the incenter. By the Angle Bisector Theorem B D D C A B A C.

The angle bisector of an angle of a triangle is a straight line that divides the angle into two congruent angles. Q R S P 1 2 26 Each figure shows a triangle with its three angle bisectors intersecting at point P. The angle bisector of an angle.

What is the Angle Bisector theorem. MBОOBF as ВК is the bisector of angle В. 8892 Name _____ Class _____ In this activity you will explore.

ВО is the common hypotenuse. The length of the bisector of angle in the above triangle is given by. The incenter is equidistant from the sides of the triangle.

11-12 is the line or line segment that divides the angle into two equal parts. Every triangle has three angle bisectors. In a triangle an angle bisector is a line which bisects an angle of the triangle.

So we get angle ABF angle BFC alternate interior angles are equal. The angle bisectors meet at the incenter which has trilinear coordinates 111. An angle bisector of a triangle is a line segment that bisects a vertex angle of a triangle and meets the opposite side of the triangle when extended.

The point of concurrency of the angle bisectors is called the incenter of the triangle and it always lies inside the triangle. Triangle vertices are usually named A B and C. An angle bisector divides an angle.

We know that BD is the angle bisector of angle ABC which means angle ABD angle CBD. As you can see in the picture below the angle bisector theorem states that the angle bisector like segment AD in the picture below divides the sides of the a triangle proportionally. An angle bisector in a triangle is a segment drawn from a vertex that bisects cuts in half that vertex angle.

This video introduced an angle bisector and states the properties of the angle bisectors or a triangleComplete Video List. This online calculator computes the length of the angle bisector given the lengths of triangle edges see the picture. That is the edge between A and B is named c between A and C -.

According to the property of congruent triangles. Draw B E A D. It has been illustrated in the diagram shown below.

By the Side-Splitter Theorem. They are also called the internal bisector of an angle. The interior bisector of an angle also called the internal angle bisector Kimberling 1998 pp.

1 mSUT 34. 3 PT 3. In Figure is an.

Triangle edges - a b c where the letter denotes opposite vertex. U S P T 1 2 17 2 Find mSQR if m2 13. Same as angle ABF.

An angle bisector divides an angle into two equal parts. This video shows how to construct the angle bisectors of a triangle using a compass and straightedgeComplete Video List. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.

Now CF is parallel to AB and the transversal is BF. The proportional relationship that occurs when an angle bisector in a triangle divides the opposite side. But we already know angle ABD ie.

Extend C A to meet B E at point E. According to the definition of perpendicular bisector it is a line that divides a line segment into two equal parts and is also perpendicular to it. F E D S T U P 3 4 Find PV if.

Read more »

How To Find The Leg Of A Triangle With The Hypotenuse

What is the area of the triangle. See the solution with steps using the Pythagorean Theorem formula.

7dlgc Lftcb3sm

Knowledge of the ratio o.

How to find the leg of a triangle with the hypotenuse. In fact if we know the lengths for any two sides leg A leg B and hypotenuse C we can easily figure out the missing side by applying the formula. A 2 B 2 C 2 A and B are the lengths of the legs of the triangle. Enter a and b then click Calculate Hypotenuse button.

In the triangle above you are given measures for legs a. Solution for The leg of a right triangle is 10in and the hypotenuse is 26in. If you only know the length of the hypotenuse you will not be able to proceed.

In any right triangle the area of the square whose side is the hypotenuse the side opposite the right angle is equal to the sum of the areas of the squares whose sides are the two legs the two sides that meet at a right angle. C a sin α b sin β from the law of sines. The legs of a right triangle are the sides that are adjacent to its right angle.

Calculates the angle and hypotenuse of a right triangle given the adjacent and opposite. The hypotenuse leg theorem is a criterion used to prove whether a given set of right triangles are congruent. The Pythagorean Theorem tells us that the relationship in every right triangle is.

A special right triangle is a right triangle having angles of 30 60 90 or 45 45 90. How to use this tool. Given area and one leg.

This allows us to always figure out the third side of a triangle if we know two. Length of Hypotenuse² Length of side 1² Length of side 2². We can use the Pythagorean theorem to find a missing leg of a triangle but only if we know the length measure of the hypotenuse and the other one of the legs.

1 costhetalarge fracac hspace20pxsinthetalarge fracbc hspace20pxtanthetalarge fracba. The hypotenuse leg HL theorem states that. AB XZ hypotenuse reason.

You can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangles other two sides called the legs. The Pythagorean Theorem states. C a² b² Given angle and one leg.

This can help you find any missing side. C is the hypotenuse. Take a square root of sum of squares.

As area of a right triangle is equal to a b 2 then. The formula for area of a right triangle is. A right triangle consists of two legs and a hypotenuse.

To calculate the hypotenuse use the pythagorean theorem as follows. Lets start to understand how to find hypotenuse and the length of the longest side of a right-angled triangle with the help of the hypotenuse. The hypotenuse of a triangle calculator can be determined hypotenuse by using either two sides one angle and side or area and one side of a right-angled triangle.

The red one is the 45 45 90 degree angle triangle. The hypotenuse is the side of the triangle opposite the right angle. C a² b² a² area 2 a² area 2 b² b².

Sometimes we have problems that ask us to find a missing length of one of these legs. This calculator also finds the area A of the right triangle with sides a and b. A given set of triangles are congruent if the corresponding lengths of their hypotenuse and one leg are equal.

The legs of such a triangle are equal the hypotenuse is calculated immediately from the equation c a2. If the hypotenuse value is given the side length will be equal to a c22. Put another way if you know the lengths of a and b you can find c.

Given AC ZY leg reason. And then theres the hypotenuse leg theorem or HL theorem. A 2 b 2 c 2.

If you know the angle of 1 vertice - other than the right angle - you can use this knowledge and trigonometry to find the length of the third angle as well as the length of the length of the two legs. Learn about the special right triangles. For right triangles only enter any two values to find the third.

Given ABC XYZ by the hypotenuse leg theorem which states that two right triangles are congruent if their hypotenuses are congruent and a corresponding leg is congruent. Because of the Pythagorean Theorem it is easy to find the hypotenuse of a right triangle if we are given the sides of a right triangle. The two legs meet at a 90 angle and the hypotenuse is the longest side of the right triangle and is the side opposite the right angle.

Read more »

Asa Triangle Congruence Postulate Examples

We can say that two triangles are congruent if any of the SSS SAS ASA or AAS postulates are satisfied. TRIANGLE CONGRUENCE FOR G8 SSS SAS ASA RHS - Detailed Discussion Examples l Your Math GuruVideo Content.

Proofs With Similar Triangles A Plus Topper Https Www Aplustopper Com Proofs Similar Triangles Theorems Different Types Of Triangles Similar Triangles

Side Side SideSSS Angle Side Angle ASA Side Angle Side SAS Angle Angle Side AAS Hypotenuse Leg HL CPCTC.

Asa triangle congruence postulate examples. The Hypotenuse-Leg HL Rule states that. This is one of them ASA. In this case we know that two corresponding angles are congruent B Y and C Z and corresponding segments not in between the angles are congruent AB XY.

Use the same diagram of ASA from Congruent Triangles article. Since all the angles and segments match up to each corresponding location on the triangles we can say that ABC X. Correct Answer is.

If two angles and the included side of one triangle are congruent to the two angles and the included side of another triangle then the two triangles are congruent. It explains how to prove if two triangles are congruent using. I can prove triangles congruent using ASA and AAS.

A B C X Y Z. We have MAC and CHZ with side m congruent to side c. This video is about Triangle Con.

Corresponding Parts ABC DEF B A C E D F AB DE BC EF AC DF A D B E C F Example 1 Do you need all six. Congruent Triangles Section 4-5. If any two angles and the included side are the same in both triangles then the triangles are congruent.

Triangle Congruence Theorems SSS SAS ASA Postulates Triangles can be similar or congruent. Try thisDrag any orange dot at PQR. Corresponding Sides and Angles.

These two triangles are congruent because two sides and the included angle are congruent. The other triangle LMN will change to remain congruent to the triangle PQR. If two angles and the included side of one triangle are equal to two angles and the included side of another triangle then the two triangles are congruent.

As CAB ACD AC AC and ACB CAD by ASA Postulate we have ΔACB ΔCAD. In the right triangles ΔABC and ΔPQR if AB PR AC QR then ΔABC ΔRPQ. What were going to do in this video is show that if we have two different triangles that have one pair of sides that have the same length so these blue sides in each of these triangles have the same length and they have two pairs of angles where for each pair the corresponding angles have the same measure so this gray angle here has the same measure as this angle here and then these double.

States that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle then the two triangles are congruent. A is congruent to H while C is congruent to Z. Proving Congruence ASA and AAS SOL.

Similar triangles will have congruent angles but sides of different lengths. Testing to see if triangles are congruent involves three postulates abbreviated SAS ASA and SSS. If two angles and the included side of a triangle are congruent to two angles and the included side of another triangle then the two triangles are congruent.

If BAC FEG AC EG BCA FGE then ΔABC ΔEFG. C A B Z X Y angle AB XY side A C B X Z Y angle Worksheet Activity on Angle Side Angle. By the ASA Postulate these two triangles are congruent.

Their interior angles and sides will be congruent. G5 The student will b prove two triangles are congruent or similar given information in the form of a figure or statement using algebraic and coordinate as well as deductive proofs. Use the ASA Postulate to test for triangle congruence Use the AAS Theorem to test for triangle congruence.

Congruence If all six pairs of corresponding parts sides and angles are congruent then the triangles are congruent. Congruent triangles will have completely matching angles and sides. If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle then the two right triangles are congruent.

For a list see Congruent Triangles. Angle-Side-Angle ASA Congruence Postulate. ASA Postulate Example Angle-Angle-Side Whereas the Angle-Angle-Side Postulate AAS tells us that if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle then the two triangles are congruent.

This geometry video tutorial provides a basic introduction into triangle congruence theorems. Two geometric figures with exactly the same size and shape. Example of Angle Side Angle Proof.

ASA SAS SSS Hypotenuse Leg Preparing for Proof.

Read more »

What Is Opposite Adjacent And Hypotenuse In A Triangle

1 Identify the parts of this triangle 1 point 11 8 x reference angle 8 adjacent side. What is the length of the side adjacent to A.

Sine Cosine Tangent Diagram For Help On How To Identify The Adjacent Opposite And Hypotenuse Studying Math Math Methods Teaching Math

11 hypotenuse x reference angle 8 opposite side 11 hypotenuse x opposite 8 adjacent side 11 hypotenuse O x reference angle 8 hypotenuse 11 adjacent side 1 point 2 Based on your labels to number 1 determine what trig function you will use to solve for x.

What is opposite adjacent and hypotenuse in a triangle. The adjacent is the side that forms the angle of choice along with the hypotenuse. Learn all about the trigonometry of right triangles. 4 How do we create a right triangle when given a trig ratio.

Hypotenuse opposite leg and adjacent leg. In each triangle label the appropriate sides as adjacent opposite and hypotenuse with respect to the marked acute angle. Sine of an angle is always the ratio of the fracopposite sidehypotenuse.

We use special words to describe the sides of right triangles. The side PQ which is opposite to the right angle PRQ is called the hypotenuse. If we take ABC as a triangle right angled at B say then AC is called the hypotenuse.

Use SOHCAHTOA 4 sin 8 5 opposite k hypotenuse 3 cos 6 5 adjacent k hypotenuse 4 tan 133 3. If you want to calculate hypotenuse enter the values for other sides and angle. Calculates the adjacent and opposite of a right triangle given the angle and hypotenuse.

The side opposite to the right angle is called the hypotenuse. х 11 8 inverse sin inverse. If we consider the angle A for trigonometric ratios the BC is called the opposite side and AB is called the adjacent side.

The hypotenuse is the longest side of the right triangle. The side RQ is called the adjacent side of angle θ. We use special words to describe the sides of right triangles.

Tan q Opposite Adjacent. Sin q Opposite Hypotenuse. The hypotenuse of a right triangle is always the side opposite the right angle.

The adjacent and opposite can only be found if you choose one of the non right angled angles. Find the longest side and label it the hypotenuse. In a right triangle the hypotenuse is the longest side an opposite side is the one across from a given angle and an adjacent side is next to a given angle.

Cos q Adjacent Hypotenuse. 3 What are the reciprocal trig functions. Sineangle frac textopposite sidetexthypotenuse Example 1.

In a right triangle the hypotenuse is the longest side an opposite side is the one across from a given angle and an adjacent side is next to a given angle. 2 How do we find a missing side or angle of a right triangle. The hypotenuse of a right triangle is always the side opposite the right angle.

A Opposite X. A right triangle is a triangle that has 90 degrees as one of its angles. The right angle square always points to the.

What is the longest side. The adjacent and the opposite sides depend on the angle θ. The side PR is called the opposite side of angle θ.

Select what angle sides you want to calculate then enter the values in the respective rows and click calculate. The opposite is the side that does not form the angle of choice. Adjacent B hypotenuse tan opposite B adjacent Model Problem 1 Identify The side adjacent opposite to angle x and the hypotenuse Adjacent to x.

C Model Problem 2 What is sin k cos k and tank. The longest side of a right triangle. What are the 3 trigonometry ratios.

The formulae formula for finding angle and sides of triangle can be easily remembered using the sentence - O ld H arry A nd H is O ld A unt Sin q OldHarry OppositeHypotenuse Cos q AndHis AdjacentHypotenuse Tan q OldAunt OppositeAdjacent. Hi guys welcome to my channel this is mre143 in this video we are going learn kung paano makuha ang opposite adjacent or hypotenuse side given ang isang.

Read more »

Substitution Property Of Equality Triangle

Reflexive property of congruence. Figure A figure A.

Pin On Celestial Teaching Learning

This geometry video tutorial provides a basic introduction into the transitive property of congruence and the substitution property of equality.

Substitution property of equality triangle. AA similarity theorem Which reason is missing in step 2. Closing 1 minute Would you prefer to prove that the base angles of an isosceles triangle are equal in measure using transformations or by using SAS. Substitution property of equality.

Reflexive pretty much means something relating to itself. If a b then a can be substituted for b in any equation or inequality Subtraction Property of Equality. A quantity may be substituted for its equal in any expression.

Subtraction Property of Equality 11. Triangle Sum Theorem C. Triangle ABC triangle ADF Statement.

Property of Equality AB 5 2 pAM Distributive property 90 Chapter 2 Segments and Angles a1 and a2 are both supplementary to a3. ACB is an obtuse angle. If angles are equal then they are congruent 8.

If you ever plug a value in for a variable into an expression or equation youre using the Substitution Property of Equality. The entire sides are actually and. 80 mK 180 4.

A conjecture and the flowchart proof used to prove the conjecture are shown. Drag an expression or phrase to each box to complete the proof. Postulates of Equality and Operations Addition Property of Equality.

Mwmxmz The exterior angle of a triangle equals the sum of the two opposite interior angles. Subtraction property of equality 6. Mxmy Vertical angles are equal in measure.

Then mP 25 and mQ 25. Since the sum of the angles measure is 180 we can write the equation below. Note that and arent sides of the triangles but rather part of the side length.

5 - definition of a right angle. Mwmxmz180 Substitution property of equality. Angle sum theorem Substitution property of equality Subtraction property of equality.

Ultimate Math Solver Free. Mp mQ mR 180 25 25 mR 180 mR 130 The measure of the third angle is 130. Division Property of Equality G.

If a b then a - c b - c Properties of Lines and Angles. If two geometric objects segments angles triangles or whatever are congruent and you have a statement involving one of them you can pull the switcheroo and replace the one with the other. K N 7.

MK 100 5. Mwmymz Substitution property of equality.

When the base angles of a triangle are equal in measure the triangle is isosceles. Definition of obtuse angle An obtuse angle is an angle of greater than 90 and less than 180 7. Angle ABC cong angle ADF What is the reasonjustification.

We know that because of the reflective property. The base the triangle will be equal to the triangle and the remaining angles will be equal to the remaining angles respectively namely those which the equal sides subtend. Reflexive property of congruence.

Note that you will not be able to find the term switcheroo in your geometry glossary. If ab then b can be substituted for a in any expression. Given the diagram to the right prove that mwmymz.

MDEG 51 mGEF 39 - 1 mDEG mGEF mDEF - 2 3 - Substitution Property of Equality. If a b then a c b c Substitution Property of Equality. What is reflexive property.

The length of a leg of a right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse adjacent to that leg. Show that a1 ca 2. Both overlap the line segment.

Substitution property of equality. The substitution property of equality. Solution ma1 1 ma3 5 180 8 Definition of supplementary angles ma2 1 ma3 5 180 8 Definition of supplementary angles ma1 1 ma3 5 ma2 1 ma3 Substitution Property of Equality ma1 5 ma2 Subtraction.

MACB120 Subtract 60 from the both sides Subtraction Property of Equality Subtraction property of equality says that if we subtract from one side of an equationthen it must be subtracted from the other side of the equation to keep the equation the same 6. If a b then a c b c Multiplication Property of Equality. MK mN 6.

HKJ LNP 8. M1 m2 m3 180 Substitution property of equality Label the vertices of the triangle P Q and R. This property allows you to substitute quantities for each other into an expression as long as those quantities are equal.

The substitution property of equality one of the eight properties of equality states that if x y then x can be substituted in for y in any equation and y can be substituted for x in any equation.

Read more »

What Are The Attributes Of A Right Triangle

Comparing Angles to Right Angles 4 Estimate Measure and Compare Angles Using Degrees 5 Angles on a Straight Line 6 Angles On a Point 6 Vertically Opposite Angles 6 Classifying Triangles and Describing Quadrilaterals 7 Angle Sum of a Triangle 7 Parallel Lines 7 Corresponding Alternate and Co-Interior Angles 7 Area and Perimeter. However considering soft skills merely as important attributes that the project manager is expected to employ in the main task of finding a trade-off among the components of the iron triangle just leads to a set of good advice and reasonable suggestions eg be yourself pay attention to team members as individuals be.

Right Angled Triangle Definition Properties Formulas

Read more »

Reflexive Property Of Equality Triangle

The reflexive property of equality means that all the real numbers are equal to themselves. Enjoy the videos and music you love upload original content and share it all with friends family and the world on YouTube.

Properties Of Equality Lymoore209 Algebraic Proof Properties Of Addition Subtraction

The reflexivity is one of the three properties that define the equivalence relation.

Reflexive property of equality triangle. Hence the above are the reasons of the statements in given proof. Triangles BCA and DAC are. Reflexive Property of Equality Part 2.

Or in other words. ΔABC is a right triangle. AD BC BCAE ADBE Prove.

The Reflexive Property of Equality states that any quantity is equal to greater than less than itself. Statement Justificatio n Draw an altitude from point C to Let BC a CA b AB c CD h DB y AD x y x c ca equals ay and cb equals bx a 2 cy. AXBX Given 3 4 90 both right angles CXCX Common i.

It is congruent to itself by the Reflexive Property of Equality. Similar triangles will look like they have either been shrunk or puffed up in size. B 2 cx a 2 b 2 cy b 2 a 2.

For example in the assembly line of cars or TV sets the same part needs to fit into each unit that comes down the assembly line. Having congruent parts available in the market also allows for easier repair and maintenance of the products. Angles BCA and DAC are congruent by the same reasoning.

Note that for all properties of an equivalence relation it doesnt matter if f is injective or f x c for some constant c. Properties of congruence and equality Learn when to apply the reflexive property transitive and symmetric properties in geometric proofs. X X f x f x so reflexivity holds ie x x R.

AXC BXC Given Reflexive Property of Equality. Triangles 3 Triangle ADE congruent to Triangle BCE 5. AB BD AB BC AC AD Prove.

What is the difference between the Reflexive Property of Equality and the Reflexive Property of Congruence. If we had a triangle with the same side lengths and angle measures the triangles would be congruent. The Reflexive Property of Congruence states that any geometric figure is congruent similar to itself.

Lets say given this diagram right over here we know that the length of segment a-b is equal to the length of AC so a B which is this whole side right over here the length of this entire side as a given is equal to the length of this entire side right over here so thats the entire side right over there and then we also know that angle a bf a bf is equal to angle AC or you could see their. Reflexive Property 3 SAS Side-Angle-Side 4 CPCTE Corresponding Parts of Congruent Triangles are Equal Given. Leg-Leg TheoremMatch the reasons with the statements in the proof to prove that triangle ABC is congruent to triangle ABD given that AB BD AB BC and AC AD.

So if the top angle of one triangle equals 45. A statement that indicates that two triangles are congruent by listing the vertices in the order of correspondence. Parts must be identical or congruent to be interchangeable.

Of Congruent Triangles 4-4 Chapter 4 216 Underline the correct words to complete each sentence. If f x c for some constant c then f x f x c. You should find that the relation you defined IS an equivalence relation.

It is used to prove the congruence in geometric figures. E reflexive property of equality Hence by SAS similarity theorem ΔAXC ΔBXC. Introduction Congruence is very important in mass production and manufacturing.

We explain Reflexive Property of Congruence and Equality with video tutorials and quizzes using our Many WaysTM approach from multiple teachers. Also all the corresponding angles will be equal to each other. A 2 b 2 c 2 The following two-column proof with missing justifications proves the Pythagorean Theorem using similar triangles.

ABC ABD 13 and 4 are right angles AX BX 2CX CX 3. Construct diagonal A C with a straightedge. When you look in the mirror you see yourself.

The reflexive property of congruence shows that any geometric figure is congruent. According to the given information and. This property is applied for almost every number.

One way to remember the Reflexive Property is that the word reflexive has the same root as reflection Reflection should make you think of a mirror. Learn which property applies to numbers and variables and which applies to lines and shapes. Likewise the reflexive property says that something is.

In the diagram above you can say that the shared side of the triangles is congruent because of the reflexive property.

Read more »

What Is Triangle Congruence Criteria

In geometry congruence criteria are the rules that allow you to prove or show or decide that two triangles are congruent. What triangle congruence criteria is shown in the given diagram.

Criteria For Congruent Triangles A Plus Topper Criteriaforcongruenceoftriangles Positivity Chart Topper

Two triangles are congruent if two angles and the included side.

What is triangle congruence criteria. There are 5 main rules of congruency for triangles. ASA Angle Side Angle Congruence Criteria Condition. To learn more about Triangles enrol in our full course now.

Answer choices COB COA AOD AOC COB. HttpsbitlyTriangles_DMIn this video we will learn. Two triangles are congruent if three sides of one triangle are.

The triangles are congruent when the lengths of three sides of one triangle are equal to the lengths of corresponding sides of the other triangle. Angle-Side- Angle AAS Criterion. Which are pairs of vertical angles.

Congruent is math-speak for identical The congruence criteria allow you to decide based on a pretty small amount of information that two triangles are congruent. Proving the SAS triangle congruence criterion using transformations Proving the ASA and AAS triangle congruence criteria using transformations This is the currently selected item. What is the value of x.

Report an issue. Right trianglesare congruent if the hypotenuseand one corresponding leg are equal in both triangles. AAS Angle Angle Side Congruence Criteria.

These four criteria used to test triangle congruence include. SSS Side Side Side Congruence Criteria Condition. This is one of them HL.

There are more ways to prove the congruency of triangles but in this lesson we will restrict ourselves to these postulates only. There are five ways to test that two triangles are congruent. 000 SAS condition for Congruence032 tw.

Congruence Criteria It turns out that knowing some of the six congruences of corresponding sides and angles are enough to guarantee congruence of the triangle and the truth of all six congruences. Triangle QPR is congruent to triangle SPR as shown in the figure. It is called Side-Side-Side SSS criterion for.

Side Side Side SSS Side Angle Side SAS Angle Side Angle ASA and Angle Angle Side AAS.

Read more »

Does Aas Prove Triangle Congruence

We discuss how to approach two col. Choose 5 key terms from this unit that you.

Triangle Congruence 4 Mazes Sss Sas Asa Aas Hl From Math Resources And Activities On Teache Teaching Geometry Geometry Lessons High School Math Teacher

Geometry A Unit 6 Congruent Triangles I.

Does aas prove triangle congruence. RST UVT Angle-Side-Angle ASA Congruence Postulate If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle then the two triangles are congruent. The ASA criterion for triangle congruence states that if two triangles have two pairs of congruent angles and the common side of the angles in one triangle is congruent to the corresponding side in the other triangle then the triangles are congruent. Proving Triangles are Congruent.

Prove that triangles are congruent using the ASA Congruence Postulate and the AAS Congruence Theorem 2. AAS Postulate Angle-Angle-Side If two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle then the triangles are congruent. If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle the triangles are congruent.

SSS and SAS SSS AND SAS C ONGRUENCE P OSTULATES. Follow along with this tutorial to see an example. There are five ways to test that two triangles are congruent.

This is one of them AAS. If they are then you know that the corresponding parts are congruent. The AAS Theorem says.

For a list see Congruent Triangles. Worksheet Activity on the Angle Angle Side Postulate. Angle-Angle-Side AAS Congruence Theorem If two angles and a non-included side of one triangle are.

Learn how to do a 2 column proof proving triangles congruent by AAS in this video math tutorial by Marios Math Tutoring. In order to use this postulate it is essential that the congruent sides not be included between the. Notice how it says non-included side meaning you take two consecutive angles.

Use congruence postulates and theorems in real-life problems. Suppose we have two triangles ABC and DEF where B E Corresponding sides C F Corresponding sides And. If there are two pairs of corresponding angles and a pair of corresponding opposite sides that are equal in measure then the triangles are congruent.

These theorems do not prove congruence to learn more click on the links Corresponding Sides and Angles AAA only shows similarity SSA Does not prove congruence. If Angle aA c aD Side AC c DF and Angle aC c aF then TABC c TDEF. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle then the triangles are said to be congruent.

If youre given information about two triangles and asked to prove parts of the triangles are congruent see if you can show the two triangles are congruent. Triangle are congruent to two angles and the included side of a second triangle then the two triangles are congruent. ANGLE-ANGLE-SIDE AAS CONGRUENCE THEOREM If two angles and a nonincluded side of one triangle are congruent to two angles and the corresponding nonincluded side.

AAS congruency can be proved in easy steps. Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangles. Proving Congruent Triangles with AAS The Angle Angle Side postulate often abbreviated as AAS states that if two angles and the non-included side one triangle are congruent to two angles and the non-included side of another triangle then these two triangles are congruent.

Identify congruent figures and corresponding parts of congruent figures Prove that two triangles are congruent using various methods such as SSS SAS ASA AAS and HL Prove that parts of two triangles are congruent Identify and use properties of isosceles and equilateral triangles II. It means that just because two triangles have congruent corresponding angles it does not prove the triangles are congruent.

Read more »