What Does Reflexive Property In Math Mean

Symmetric Property The Symmetric Property states that for all real numbers x and y if x y. Given a relation R we dont have a sufficient information to decide whether or not it is reflexive.

Reflexive Photo By Cralgebraii Photobucket Light In The Dark Math Boards Math

In the area of mathematics known as functional analysis a reflexive space is a locally convex topological vector space TVS such that the canonical evaluation map from X into its bidual which is the strong dual of the strong dual of X is an isomorphism of TVSs.

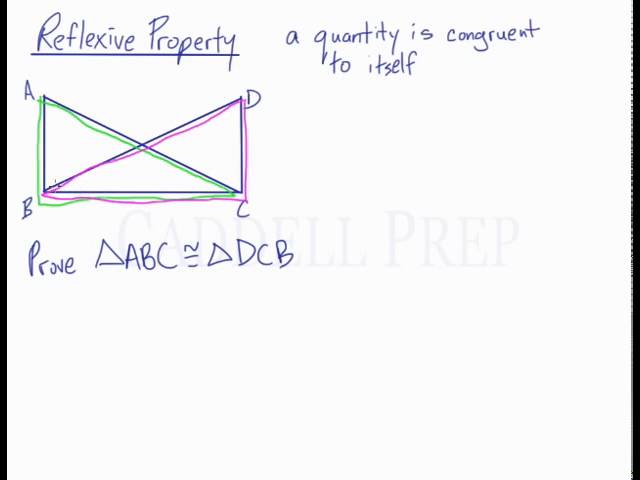
What does reflexive property in math mean. Reflexive rĭ-flĕk sĭv Of or relating to a mathematical or logical relation such that for any given element that element has the given relation to itself. Reflexive Relation In Maths a binary relation R across a set X is reflexive if each element of set X is related or linked to itself. Reflexive Property The Reflexive Property states that for every real number x x x.

The Reflexive Property of Congruence tells us that any geometric figure is congruent to itself. Thus a-a is even. The symmetric property states that for any real numbers a and b if a b then b a.

The reflexive property states that any quantity is equal to itself so Y equals Y. Hence R is Reflexive. The reflexivity is one of the three properties that define the equivalence relation.

Therefore every angle is congruent to itself. The reason is that we say that R is reflexive on A rather than just reflexive. The reflexive property of mathematics states that aa or that any number is always equaled to itselfExamples1 15 5-10² -10² which property can you use to prove that ME is congruent to.

The reflexive property of equality means that all the real numbers are equal to themselves. From the given relation a a 0 0. The reflexive property states that any real number a is equal to itself.

Congruence means the figure has the same size and shape. Pictures and examples explaining the most frequently studied math properties including the associative distributive commutative and substitution property. A line segment angle polygon circle or another figure of the given size and shape is self-congruent.

Reflexive Property. The substitution postulate states that if H equals B then H may be substituted for B and B may be substituted for H in any equation. Symmetry and transitivity on.

That is a a. Angles have a measurable degree of openness so they have specific shapes and sizes. Associative Distributive Reflexive Commutative and more.

A relation is said to be a reflexive relation on a given set if each element of the set is related to itself. From the given relation a b b a We know that a b -b a b a Hence a. The reflexive property states that some ordered pairs actually belong to the relation R or some elements of A are related.

It is an integral part of defining even equivalence relations. This property is applied for almost every number. Equality in mathematics is a reflexive relation since a a.

The symmetric property states that if J equals K then K equals J. Speaking very informally reflexivity is fundamentally different in nature from the symmetry and transitivity because it is the only property that actually requires specific ordered pairs to be in a relation. Thus it has a reflexive property and is said to hold reflexivity.

Therefore a a belongs to R. Let us take a relation R in a set A. In terms of relations this can be defined as a a R a X or as I R where I is the identity relation on A.

The other two only require that ifsome ordered pairs are in there. The reflexive property of congruence states that any geometric figure is congruent to itself. Reflexive relation is an important concept to know for functions and relations.

And 0 is always even. It is used to prove the congruence in geometric figures. The relation 0 0 is certainly not reflexive as a relation on N but it is reflexive as a relation on 0.

The reflexive property has a universal quantifier and hence we must prove that for all x A x R x. Reflexivity is not an internal property of a relation.

Read more »

Property Of Operations In Math

Commutative property of multiplication When two or more numbers are multiplied the order of the numbers does not change the product. PEMDAS is an acronym that may help you remember order of operations for solving math equations.

Free Properties Of Operations Cards For Your Math Word Wall Math Word Walls Math Words Word Wall Cards

Properties of Operations are the foundation of arithmetic.

Property of operations in math. Multiplication of whole numbers distributes over addition The number 1 is an identity for multiplication of whole numbers. Properties of Operations Quiz. In order to apply the distributive property it must be multiplication outside the parentheses and either addition or subtraction inside the parentheses.

Here are the four properties youll think about. In numbers this means 2 3 3 2. After submitting the quiz please click the REVIEW button to view the corrections.

What a mouthful of words. Operations properties a series of properties rules or laws associated with mathematical operations and equality. This video describes some of the common properties of operations.

A property of two operations. For addition the rule is a b b a. Properties Of Operation Displaying top 8 worksheets found for - Properties Of Operation.

Zero Identity Commutative Distributive 2 differentiation options and Associative. Together to use properties operations math workshop because its correct name the associative the ccss listed or tape cards of operations have properties. The word commutative comes from commute or move around so the Commutative Property is the one that refers to moving stuff around.

Properties Of Operations 7th Grade - Displaying top 8 worksheets found for this concept. Some of the worksheets for this concept are Properties of operations math work for grade 7 at Using order of operations Order of operations pemdas practice work Word problem practice workbook Sample work from Properties of operations Order of operations Using the distributive property date period. 2 5 5 2.

PEMDAS is typcially expanded into the phrase Please Excuse My Dear Aunt Sally The first letter of each word in the phrase creates the PEMDAS acronym. Powered by Create your own unique website with customizable templates. RATIONAL NUMBERS Types of rational numbersproperties of rational numbers Operation of Rational numbersRational numbers.

Solve math problems with the standard. The Commutative Laws say we can swap numbers over and still get the same answer. Some of you may be wondering exactly what they mean.

This video describes some of the common properties of operations. Commutative property of addition When two or more numbers are added the order of the numbers does not change the sum. Commutative Associative and Distributive Laws.

Math Order of Operations - PEMDAS BEDMAS BODMAS. Some of the worksheets for this concept are Properties of operations math work for grade 7 at Properties of exponents Properties and operations of fractions Properties of logarithms Using order of operations Exercise work Sets and set operations. The distributive property is the process of passing the number value outside of the parentheses using multiplication to the numbers being added or subtracted inside the parentheses.

Multiplication of whole numbers is commutative. Formal terms for the product of operations in front of the math. Properties of Multiplication 7 Day Unit 3OA5 This 7-day unit is designed for your students to learn about 5 different properties of multiplication.

But the ideas are simple. Multiplication of whole numbers is associative. The properties taught in this unit are.

A Math Dictionary for Kids. In numbers this means 23 32. We use them when performing computations and recalling basic facts.

For multiplication the rule is ab ba. Lot of multiplication of math simplify expressions without even have a property. Multiplication Properties of Operations are those three pesky words that reoccur throughout the common core standards.

PROPERTIES OF OPERATIONSThis episode teaches how to find the missing number in an equation involving properties of operationsSubscribe.

Read more »

What Is Reflexive Property In Math Terms

Also known as the reflexive building of equal rights it is the basis for many mathematical principles. The formula for this property is a a.

Reflexive Property Of Congruence Algebra And Geometry Help

Pictures and examples explaining the most frequently studied math properties including the associative distributive commutative and substitution property.

What is reflexive property in math terms. We learned that the reflexive property of equality means that anything is equal to itself. Because V consists of only two ordered pairs both of them in the form of a a V is transitive. Thus it has a reflexive property and is said to hold reflexivity.

Reflexive propertysimply states that any numberis equal to itself. A number equals itself. In algebra the reflexive property of equality states that a number is always equal to itself.

This property is applied for almost every number. Reflexive pretty much means something relating to. Symmetric Property The Symmetric Property states that for all real numbers x and y if x y.

Examples of reflexive property of equality. The Reflexive Property of Congruence tells us that any geometric figure is congruent to itself. Reflexive property of equality.

Associative Distributive Reflexive Commutative and more. The property that a a. Given that the reflexive property of equal rights says that a a we can use it to do several things with algebra to assist us in addressing equations.

In math the reflexive property tells us that a number is equal to itself. It is used to prove the congruence in geometric figures. Reflexive Property The Reflexive Property states that for every real number x x x.

Since the reflexive property of equality says that a a we can use it do many things with algebra to help us solve equations. Check if R follows reflexive property and is a reflexive relation on A. The reflexivity is one of the three properties that define the equivalence relation.

This property tells us that any number is equal to itself. Examples of the Reflexive Property. Reflexive property for all real numbers x x x.

In geometry the reflexive property of congruence states that an angle line segment or shape is always congruent to itself. Reflexive Relation In Maths a binary relation R across a set X is reflexive if each element of set X is related or linked to itself. Reflexive Relation Examples.

Therefore V is an equivalence relation. The relation V is reflexive because 0 0 V and 1 1 V. DM me your math problems.

Two numbers are only equal to each other if and only if both the numbers are same. Therefore every angle is congruent to itself. Reflexive Property of Equality.

Angles have a measurable degree of openness so they have specific shapes and sizes. In mathematics the reflexive property tells us that a number is equal to itself. Reflexiveproperty simply states that any number is equal to itself.

You could look at the reflexive property of equality as when a number looks across an equal sign and sees a mirror image of itself. A relation R is on set A set of all integers is defined by x R y if and only if 2x 3y is divisible by 5 for all x y A. Reflexiveproperty for all real numbers x x x.

Now 2x 3x 5x which is divisible by 5. One of the equivalence properties of equality. The reflexive property of equality means that all the real numbers are equal to themselves.

A number equals itself. Let us consider x A. Httpbitlytarversub Subscribe to join the best students on the planet----Have Instagram.

The reflexive property of mathematics states that aa or that any number is always equaled to itself. Also known as the reflexive property of equality it is the basis for many mathematical principles. A line segment angle polygon circle or another figure of the given size and shape is self-congruent.

In terms of relations this can be defined as a a R a X or as I R where I is the identity relation on A. Two numbers are only equal to. It is clearly symmetric because a b V always implies b a V.

If a a a is a number then a a.

Read more »

What Is A Sss Congruence In Math

In this post we are going to prove the SSS Congruence Theorem. Read the simple instructions below to successfully enjoy the objectives of this.

Congruent Triangles Sss Sas Asa Big Ideas Math Teaching Geometry Geometry Activities

M8GE-IIId-e-1 To the Learners.

What is a sss congruence in math. The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. Worksheet and Activity on Side Side Side Postulate. Similar triangles will have congruent angles but sides of different lengths.

This is one of them SSS. Side Side Side postulate states that if three sides of one triangle are congruent to three sides of another triangle then these two triangles are congruent. Congruent Triangles - Three sides equal SSS Definition.

From this and using other postulates of Euclid we can derive the ASA and SSS criterion. Tara at pag-usapan natin kung paano ang pro. Proving Statements SSS Congruence PostulateOne on Juan Tutorial ba ang hanap mo.

For ASA criterion we cut one of the sides so as to make it equal to corresponding part of the other triangle and then derive contradiction. The proof proceeds generally by contariction. Before starting the module I want you to set aside other tasks that will disturb you while enjoying the lessons.

In a simpler way two triangles are congruent if they have the same shape and size even if their position and orientation are different. The SAS criterion for congruence is generally taken as an axiom. The SSS Similarity Rule.

Congruent triangles will have completely matching angles and sides. The triangles are congruent when the lengths of three sides of one triangle are equal to the lengths of corresponding sides of the other triangle. The learner illustrates the SAS ASA and SSS congruence postulates.

Triangles are congruent if all three sides in one triangle are congruent to the corresponding sides in the other. Congruence is the term used to define an object and its mirror image. If all three sides in one triangle are the same length as the corresponding sides in the other then the triangles are.

_____ YR SEC. SSS Congruence Rule The Side-Angle-Side theorem of congruency states that if two sides and the angle formed by these two sides are equal to two sides and the included angle of another triangle then these triangles are said to be congruent. TAGALOG Grade 8 Math Lesson.

Two triangles are congruent if both their corresponding sides and angles are equal. For a list see Congruent Triangles. There are five ways to test that two triangles are congruent.

Recall that the theorem states that if three corresponding sides of a triangle are congruent then the two triangles are congruent. Triangle Congruence Theorems SSS SAS ASA Postulates Triangles can be similar or congruent. Also learn about Congruent Figures here.

Two objects or shapes are said. SSS Criterion stands for side side side congruence postulate. In geometry two figures or objects are congruent if they have the same shape and size or if one has the same shape and size as the mirror image of the other.

TAMONDONG MATH 8 QUARTER 3 WEEK 4 P a g e 1 10 NAME. Before proving the SSS Congruence theorem we need to understand several concepts that are pre-requisite to its proof. It is called Side-Side-Side SSS criterion for.

The corresponding parts of congruent triangles are. Under the SSS theorem if all the three sides of one triangle are equal to the three corresponding sides of another triangle the two triangles are congruent.

Read more »